নিজে করি 19.3 ক্লাস 6 || Nije Kori 19.3 Class 6 || WBBSE Class 6 Chapter 19.3 Math Solution in Bengali || West Bengal Board Class 6 Chapter 19.3 Math Solution || সময়ের পরিমাপ 19.3 অধ্যায়ের সমাধান || || পশ্চিমবঙ্গ বোর্ডের ক্লাস Six অঙ্কের 19.3 অধ্যায়ের সমাধান || পশ্চিমবঙ্গ বোর্ডের ক্লাস সিক্সের অঙ্কের 19.3 অধ্যায়ের সমাধান
Share this page using :
WBBSE Class 6 Chapter 19.3 Math Solution in Bengali || Nije Kori 19.3 Class 6 || পশ্চিমবঙ্গ বোর্ডের ক্লাস Six অঙ্কের 19.3 অধ্যায়ের সমাধান || পশ্চিমবঙ্গ বোর্ডের ক্লাস সিক্সের অঙ্কের 19.3 অধ্যায়ের সমাধান
নিজে করি - 19.3
WBBSE Class 6 Chapter 19.3 Math Solution in Bengali || Nije Kori 19.3 Class 6 || পশ্চিমবঙ্গ বোর্ডের ক্লাস Six অঙ্কের 19.3 অধ্যায়ের সমাধান || পশ্চিমবঙ্গ বোর্ডের ক্লাস সিক্সের অঙ্কের 19.3 অধ্যায়ের সমাধান
(1) 2010 সালের 1 ফ্রেব্রুয়ারি সোমবার ছিল। 2010 সালের 1 মার্চ কী বার এবং 2010 সালের 1 এপ্রিল কী বার ছিল হিসাব করি।
2010 সালের 1 ফেব্রুয়ারী থেকে 2010 সালের 1 মার্চ পর্যন্ত মোট দিন সংখ্যা = 28
এখন,

\(\because \) ভাগশেষ = 0
\(\therefore\) 2010 সালের 1 মার্চ সোমবার ছিল।
2010 সালের 1 ফেব্রুয়ারী থেকে 2010 সালের 1 এপ্রিল পর্যন্ত মোট দিন সংখ্যা = 28 + 31 = 59
এখন,

\(\because \) ভাগশেষ = 3
\(\therefore\) সোমবার-এর পর তিন দিন = মঙ্গলবার, বুধবার, বৃহস্পতিবার
\(\therefore\) 1 এপ্রিল 2010 বৃহস্পতিবার ছিল
এখন,

\(\because \) ভাগশেষ = 0
\(\therefore\) 2010 সালের 1 মার্চ সোমবার ছিল।
2010 সালের 1 ফেব্রুয়ারী থেকে 2010 সালের 1 এপ্রিল পর্যন্ত মোট দিন সংখ্যা = 28 + 31 = 59
এখন,

\(\because \) ভাগশেষ = 3
\(\therefore\) সোমবার-এর পর তিন দিন = মঙ্গলবার, বুধবার, বৃহস্পতিবার
\(\therefore\) 1 এপ্রিল 2010 বৃহস্পতিবার ছিল
(2) 01/02/ 2012 বুধবার ছিল। তবে নীচের তারিখগুলি কী বার ছিল হিসাব করি। 01/03/ 2012, 01/04/2012, 01/05/2012, 04/06/2012
01/02/2012 থেকে 01/03/2012 মোট দিনসংখ্যা = 29
এখন,
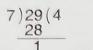
\(\because \) ভাগশেষ = 1
\(\therefore\) বুধবার-এর পরে 1 দিন = বৃহস্পতিবার
\(\therefore\) 01/03/2012 বৃহস্পতিবার ছিল।
01/02/2012 থেকে 01/04/2012 পর্যন্ত মোট দিন সংখ্যা = 29 + 31 = 60
এখন,

\(\because \) ভাগশেষ = 4
\(\therefore\) বুধবার-এর পরে 4 দিন
= বৃহস্পতিবার, শুক্রবার, শনিবার, রবিবার
\(\therefore\) 01/04/2012 রবিবার ছিল।
01/02/2012 থেকে 01/05/2012 পর্যন্ত মোট দিনসংখ্যা
= 29 + 31 + 30 = 90
এখন,

\(\because \) ভাগশেষ = 6
বুধবার-এর পরে 6 দিন = বৃহস্পতিবার, শুক্রবার, শনিবার, রবিবার, সোমবার, মঙ্গলবার
\(\therefore\) 01/05/2012 মঙ্গলবার ছিল।
01/02/2012 থেকে 01/06/2012 পর্যন্ত মোট দিনসংখ্যা
= 29 + 31 + 30 + 31 = 121
এখন,

\(\because \) ভাগশেষ 2
\(\therefore\) বুধবার-এর পরে 2 দিন = শুক্রবার
\(\therefore\) 01/06/2012 শুক্রবার ছিল।
\(\therefore\) 04/06/2012 ছিল = (শুক্রবার + 3) = সোমবার
\(\therefore\) 01/03/2012 বৃহস্পতিবার
01/04/2012 রবিবার
01/05/2012 মঙ্গলবার
04/06/2012 সোমবার
এখন,

\(\because \) ভাগশেষ = 1
\(\therefore\) বুধবার-এর পরে 1 দিন = বৃহস্পতিবার
\(\therefore\) 01/03/2012 বৃহস্পতিবার ছিল।
01/02/2012 থেকে 01/04/2012 পর্যন্ত মোট দিন সংখ্যা = 29 + 31 = 60
এখন,

\(\because \) ভাগশেষ = 4
\(\therefore\) বুধবার-এর পরে 4 দিন
= বৃহস্পতিবার, শুক্রবার, শনিবার, রবিবার
\(\therefore\) 01/04/2012 রবিবার ছিল।
01/02/2012 থেকে 01/05/2012 পর্যন্ত মোট দিনসংখ্যা
= 29 + 31 + 30 = 90
এখন,

\(\because \) ভাগশেষ = 6
বুধবার-এর পরে 6 দিন = বৃহস্পতিবার, শুক্রবার, শনিবার, রবিবার, সোমবার, মঙ্গলবার
\(\therefore\) 01/05/2012 মঙ্গলবার ছিল।
01/02/2012 থেকে 01/06/2012 পর্যন্ত মোট দিনসংখ্যা
= 29 + 31 + 30 + 31 = 121
এখন,

\(\because \) ভাগশেষ 2
\(\therefore\) বুধবার-এর পরে 2 দিন = শুক্রবার
\(\therefore\) 01/06/2012 শুক্রবার ছিল।
\(\therefore\) 04/06/2012 ছিল = (শুক্রবার + 3) = সোমবার
\(\therefore\) 01/03/2012 বৃহস্পতিবার
01/04/2012 রবিবার
01/05/2012 মঙ্গলবার
04/06/2012 সোমবার
(3) 1996 সালের 1 জানুয়ারি সোমবার ছিল। 1997 সালের 1 জানুয়ারি কী বার ছিল হিসাব করি।
1 জানুয়ারি, 1996 থেকে 1 জানুয়ারি, 1997 পর্যন্ত মোট দিনসংখ্যা
\(= 31 + 29+ 31+ 30 + 31+30 + 31 + 31 + 30 +31 +30 +31 = 366\)
এখন,
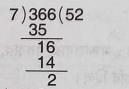
\(\therefore\) ভাগশেষ = 2
\(\therefore\) সোমবার -এর পরে 2 দিন = মঙ্গলবার, বুধবার
\(\therefore\) 1 জানুয়ারি 1997 বুধবার ছিল।
\(= 31 + 29+ 31+ 30 + 31+30 + 31 + 31 + 30 +31 +30 +31 = 366\)
এখন,
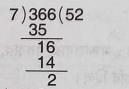
\(\therefore\) ভাগশেষ = 2
\(\therefore\) সোমবার -এর পরে 2 দিন = মঙ্গলবার, বুধবার
\(\therefore\) 1 জানুয়ারি 1997 বুধবার ছিল।
(4) 2004 সালের 1 মার্চ মোমবার। 2005 সালের 1 এপ্রিল কী বার ছিল হিসাব করি।
2004 সালের 1 মার্চ থেকে 2005 সালের 1 এপ্রিল পর্যন্ত মোট দিনসংখ্যা
\( = 31 + 30+ 31+ 30+ 31+ 31+ 30+31+30 +31 +31 +28+31 = 396\)
এখন,

\(\because \) ভাগশেষ = 4
\(\therefore\) সোমবার এর পরে 4 দিন
= মঙ্গলবার, বুধবার, বৃহস্পতিবার, শুক্রবার
\(\therefore\) 2005 সালের 1 এপ্রিল শুক্রবার ছিল।
\( = 31 + 30+ 31+ 30+ 31+ 31+ 30+31+30 +31 +31 +28+31 = 396\)
এখন,

\(\because \) ভাগশেষ = 4
\(\therefore\) সোমবার এর পরে 4 দিন
= মঙ্গলবার, বুধবার, বৃহস্পতিবার, শুক্রবার
\(\therefore\) 2005 সালের 1 এপ্রিল শুক্রবার ছিল।
(5) 2008 সালের জুন মাসের 1 তারিখ মঙ্গলবার ছিল। 2006 সালের জুন মাসের 1 তারিখ কী বার ছিল হিসাব করি।
2006 সালের 1 জুন থেকে 2007 সালের 1 জুন পর্যন্ত মোট দিনসংখ্যা
\(= 30 + 31+31+ 30+ 31+30+ 31+31+28 +31 +30 +31 = 365\)
2007 সালের 1 জুন থেকে 2008 সালের 1 জুন পর্যন্ত মোট দিনসংখ্যা
\(= 30 + 31+ 31+ 30+ 31+ 30+ 31+ 31+29+ 31+30 +31 = 366 \)
\(\therefore\) 2006 সালের 1 জুন থেকে 2008 সালের 1 জুন পর্যন্ত মোট দিনসংখ্যা \(= 365 + 366 = 731\)
এখন,

\(\because \) ভাগশেষ = 3
\(\therefore\) মঙ্গলবার-এর আগে 3 দিন = সোমবার, রবিবার, শনিবার
\(\therefore\) 2006 সালের 1 জুন শনিবার ছিল।
\(= 30 + 31+31+ 30+ 31+30+ 31+31+28 +31 +30 +31 = 365\)
2007 সালের 1 জুন থেকে 2008 সালের 1 জুন পর্যন্ত মোট দিনসংখ্যা
\(= 30 + 31+ 31+ 30+ 31+ 30+ 31+ 31+29+ 31+30 +31 = 366 \)
\(\therefore\) 2006 সালের 1 জুন থেকে 2008 সালের 1 জুন পর্যন্ত মোট দিনসংখ্যা \(= 365 + 366 = 731\)
এখন,

\(\because \) ভাগশেষ = 3
\(\therefore\) মঙ্গলবার-এর আগে 3 দিন = সোমবার, রবিবার, শনিবার
\(\therefore\) 2006 সালের 1 জুন শনিবার ছিল।
(6) 2013 সালের স্বাধীনতা দিবস বৃহস্পতিবার ছিল। 2016 সালের স্বাধীনতা দিবস কী বার হিসাব করি।
2013 সালের 15 ই আগস্ট বৃহস্পতিবার ছিল।
2013 সালের 15 ই আগস্ট থেকে 2016 সালের 15 ই আগস্ট পর্যন্ত মোট দিনসংখ্যা
\(= 365 + 365+16+ 30+ 31 +30+31+31+29+31+30+31+30+31+15=1096\)
এখন,

\(\because \) ভাগশেষ = 4
\(\therefore\) বৃহস্পতিবার-এর পরে 4 দিন
= শুক্রবার, শনিবার, রবিবার, সোমবার
\(\therefore\) 2016 সালের স্বাধীনতা দিবস সোমবার ছিল।
2013 সালের 15 ই আগস্ট থেকে 2016 সালের 15 ই আগস্ট পর্যন্ত মোট দিনসংখ্যা
\(= 365 + 365+16+ 30+ 31 +30+31+31+29+31+30+31+30+31+15=1096\)
এখন,

\(\because \) ভাগশেষ = 4
\(\therefore\) বৃহস্পতিবার-এর পরে 4 দিন
= শুক্রবার, শনিবার, রবিবার, সোমবার
\(\therefore\) 2016 সালের স্বাধীনতা দিবস সোমবার ছিল।
WBBSE Class 6 Chapter 19.3 Math Solution in Bengali || Nije Kori 19.3 Class 6 || পশ্চিমবঙ্গ বোর্ডের ক্লাস Six অঙ্কের 19.3 অধ্যায়ের সমাধান || পশ্চিমবঙ্গ বোর্ডের ক্লাস সিক্সের অঙ্কের 19.3 অধ্যায়ের সমাধান
(7) ক্যালেন্ডার দেখে 2013 সালে নীচের দিনগুলি সপ্তাহের কোন বার ছিল লিখি ও 2011 সালের এই দিনগুলি সপ্তাহের কোন বার ছিল ক্যালেন্ডার না দেখে হিসাব করে লিখি।
শিশুদিবস, শিক্ষকদিবস, গান্ধিজয়ন্তী, প্রজাতন্ত্রদিবস, নেতাজি-জয়ন্তী, বিশ্ব পরিবেশদিবস (জুন মাসের 5 তারিখ)।
শিশুদিবস, শিক্ষকদিবস, গান্ধিজয়ন্তী, প্রজাতন্ত্রদিবস, নেতাজি-জয়ন্তী, বিশ্ব পরিবেশদিবস (জুন মাসের 5 তারিখ)।
2013 সালের শিশুদিবস → 14 নভেম্বর – বৃহস্পতিবার
শিক্ষকদিবস → 5 সেপ্টেম্বর – বৃহস্পতিবার
গান্ধীজয়ন্তী → 2 অক্টোবর – বুধবার
প্রজাতন্ত্রদিবস → 26 জানুয়ারি – শনিবার
নেতাজি-জয়ন্তী → 23 শে জানুয়ারি – বুধবার
বিশ্ব পরিবেশ দিবস → 5 জুন – বুধবার
14 নভেম্বর, 2011 থেকে 14 নভেম্বর, 2012 পর্যন্ত মোট দিনসংখ্যা
\(=16+31+31+29+31+30+31+30+31 +31 + 30+ 31 +31 +30 +31 + 14 = 366\)
14 নভেম্বর, 2012 থেকে 14 নভেম্বর, 2013 পর্যন্ত মোট দিনসংখ্যা = 365
\(\therefore\) 14 নভেম্বর, 2011 থেকে 14 নভেম্বর, 2013 পর্যন্ত মোট দিনসংখ্যা \(= 366 + 365 =731\)
এখন,

\(\because \) ভাগশেষ = 3
\(\therefore\) বৃহস্পতিবার-এর আগে 3 দিন = বুধবার, মঙ্গলবার, সোমবার 14 নভেম্বর 2011 সাল সোমবার ছিল।
5 সেপ্টেম্বর 2011 সাল থেকে 5 সেপ্টেম্বর, 2013 সাল পর্যন্ত মোট দিনসংখ্যা \(= 366 + 365 = 731\)
এখন,

\(\because \) ভাগশেষ = 3
\(\therefore\) বৃহস্পতিবার-এর আগে 3 দিন = বুধবার, মঙ্গলবার, সোমবার
\(\therefore\) 2011 সালের শিক্ষকদিবস সোমবার ছিল।
2 অক্টোবর, 2011 সাল থেকে 2 অক্টোবর, 2013 পর্যন্ত মোট দিনসংখ্যা \(= 366 + 365 = 731\)
এখন,

\(\because \) ভাগশেষ = 3
\(\therefore\) বুধবার-এর আগে 3 দিন = মঙ্গলবার, সোমবার, রবিবার
\(\therefore\) 2011 সালের গান্ধীজয়ন্তী রবিবার ছিল।
26 শে জানুয়ারী, 2011 থেকে 26 শে জানুয়ারী, 2013 পর্যন্ত মোট দিনসংখ্যা \(= 366 + 365 =731\)
এখন,

\(\because \) ভাগশেষ = 3
\(\therefore\) শনিবার-এর আগে 3 দিন = শুক্রবার, বৃহস্পতিবার, বুধবার
\(\therefore\) 2011 সালের প্রজাতন্ত্রদিবস বুধবার ছিল।
23 শে জানুয়ারি, 2011 থেকে
23 শে জানুয়ারি, 2013 পর্যন্ত
মোট দিনসংখ্যা \( = 366 + 365 = 731\)
এখন,

\(\because \) ভাগশেষ = 3
\(\therefore\) বুধবার-এর আগে 3 দিন = মঙ্গলবার, সোমবার, রবিবার
\(\therefore\) 2011 সালের নেতাজি-জয়ন্তী রবিবার ছিল।
5 জুন 2011 সাল থেকে 5 জুন 2013 সাল পর্যন্ত মোট দিনসংখ্যা
\(= 366 + 365 = 731\)
এখন,

\(\because \) ভাগশেষ = 3
\(\therefore\) বুধবার-এর আগে 3 দিন = মঙ্গলবার, সোমবার, রবিবার
\(\therefore\) 2011 সালের বিশ্ব পরিবেশ দিবস রবিবার ছিল।
\(\therefore\) 2011 সালের
শিশুদিবস → 14 নভেম্বর – সোমবার
শিক্ষক দিবস → 5 সেপ্টেম্বর – সোমবার
গান্ধীজয়ন্তী → 2 অক্টোবর – রবিবার
প্রজাতন্ত্রদিবস → 26 জানুয়ারি – বুধবার
নেতাজি-জয়ন্তী → 23 শে জানুয়ারি – রবিবার
বিশ্ব পরিবেশ দিবস → 5 জুন – রবিবার।
শিক্ষকদিবস → 5 সেপ্টেম্বর – বৃহস্পতিবার
গান্ধীজয়ন্তী → 2 অক্টোবর – বুধবার
প্রজাতন্ত্রদিবস → 26 জানুয়ারি – শনিবার
নেতাজি-জয়ন্তী → 23 শে জানুয়ারি – বুধবার
বিশ্ব পরিবেশ দিবস → 5 জুন – বুধবার
14 নভেম্বর, 2011 থেকে 14 নভেম্বর, 2012 পর্যন্ত মোট দিনসংখ্যা
\(=16+31+31+29+31+30+31+30+31 +31 + 30+ 31 +31 +30 +31 + 14 = 366\)
14 নভেম্বর, 2012 থেকে 14 নভেম্বর, 2013 পর্যন্ত মোট দিনসংখ্যা = 365
\(\therefore\) 14 নভেম্বর, 2011 থেকে 14 নভেম্বর, 2013 পর্যন্ত মোট দিনসংখ্যা \(= 366 + 365 =731\)
এখন,

\(\because \) ভাগশেষ = 3
\(\therefore\) বৃহস্পতিবার-এর আগে 3 দিন = বুধবার, মঙ্গলবার, সোমবার 14 নভেম্বর 2011 সাল সোমবার ছিল।
5 সেপ্টেম্বর 2011 সাল থেকে 5 সেপ্টেম্বর, 2013 সাল পর্যন্ত মোট দিনসংখ্যা \(= 366 + 365 = 731\)
এখন,

\(\because \) ভাগশেষ = 3
\(\therefore\) বৃহস্পতিবার-এর আগে 3 দিন = বুধবার, মঙ্গলবার, সোমবার
\(\therefore\) 2011 সালের শিক্ষকদিবস সোমবার ছিল।
2 অক্টোবর, 2011 সাল থেকে 2 অক্টোবর, 2013 পর্যন্ত মোট দিনসংখ্যা \(= 366 + 365 = 731\)
এখন,

\(\because \) ভাগশেষ = 3
\(\therefore\) বুধবার-এর আগে 3 দিন = মঙ্গলবার, সোমবার, রবিবার
\(\therefore\) 2011 সালের গান্ধীজয়ন্তী রবিবার ছিল।
26 শে জানুয়ারী, 2011 থেকে 26 শে জানুয়ারী, 2013 পর্যন্ত মোট দিনসংখ্যা \(= 366 + 365 =731\)
এখন,

\(\because \) ভাগশেষ = 3
\(\therefore\) শনিবার-এর আগে 3 দিন = শুক্রবার, বৃহস্পতিবার, বুধবার
\(\therefore\) 2011 সালের প্রজাতন্ত্রদিবস বুধবার ছিল।
23 শে জানুয়ারি, 2011 থেকে
23 শে জানুয়ারি, 2013 পর্যন্ত
মোট দিনসংখ্যা \( = 366 + 365 = 731\)
এখন,

\(\because \) ভাগশেষ = 3
\(\therefore\) বুধবার-এর আগে 3 দিন = মঙ্গলবার, সোমবার, রবিবার
\(\therefore\) 2011 সালের নেতাজি-জয়ন্তী রবিবার ছিল।
5 জুন 2011 সাল থেকে 5 জুন 2013 সাল পর্যন্ত মোট দিনসংখ্যা
\(= 366 + 365 = 731\)
এখন,

\(\because \) ভাগশেষ = 3
\(\therefore\) বুধবার-এর আগে 3 দিন = মঙ্গলবার, সোমবার, রবিবার
\(\therefore\) 2011 সালের বিশ্ব পরিবেশ দিবস রবিবার ছিল।
\(\therefore\) 2011 সালের
শিশুদিবস → 14 নভেম্বর – সোমবার
শিক্ষক দিবস → 5 সেপ্টেম্বর – সোমবার
গান্ধীজয়ন্তী → 2 অক্টোবর – রবিবার
প্রজাতন্ত্রদিবস → 26 জানুয়ারি – বুধবার
নেতাজি-জয়ন্তী → 23 শে জানুয়ারি – রবিবার
বিশ্ব পরিবেশ দিবস → 5 জুন – রবিবার।
(8) (a) 1895 সাল থেকে 1915 সাল পর্যন্ত লিপইয়ারগুলি লিখি।
(b) 2010 সাল থেকে 2030 সাল পর্যন্ত লিপইয়ারগুলি লিখি।
(b) 2010 সাল থেকে 2030 সাল পর্যন্ত লিপইয়ারগুলি লিখি।

\(\because \) 1895 সালটি 4 দ্বারা বিভাজ্য নয়,
\(\therefore\) 1895 লিপইয়ার নয়।
আবার

\(\because \) 1896 সালটি 4 দ্বারা বিভাজ্য,
\(\therefore\) 1896 লিপইয়ার।
1896 সালের পরবর্তী লিপইয়ার হওয়া উচিত
1896 + 4 = 1900 কিন্তু 1900 সাল 4 দ্বারা বিভাজ্য হলেও 400 দ্বারা বিভাজ্য নয়।
তাই 1900 সালটি লিপইয়ার নয়।
\(\therefore\) 1915 সাল পর্যন্ত বাকি লিপইয়ারগুলি হল,
\(1900+4=1904, 1904+4=1908, 1908+4=1912\)
(b)

\(\because\) 2010 সালটি 4 দ্বারা বিভাজ্য নয়,
\(\therefore\) 2010 লিপইয়ার নয়।
একইভাবে 2011, 2013, 2014, 2015, 2017, 2018, 2019, 2021, 2022, 2023, 2025, 2026, 2027, 2029 লিপইয়ার নয়।
আবার,

\(\because \) 2012 সালটি 4 দ্বারা বিভাজ্য,
\(\therefore\) 2012 সাল লিপইয়ার।
\(\therefore\) 2030 পর্যন্ত বাকি লিপইয়ারগুলি হল
\(2012+ 4 =2016, 2016 + 4 = 2020,\)
\(2020 + 4 = 2024, 2024 + 4 = 2028\)
(9) আমি 2010 সাল থেকে 2013 সাল পর্যন্ত মোট চার বছর এই কলেজঘাট রোডের বাড়িতে ছিলাম। আমি মোট কতদিন কলেজঘাট রোডের বাড়িতে ছিলাম হিসাব করি।
2010 সাল থেকে 2013 সাল পর্যন্ত মোট দিনসংখ্যা
\( = 365+ 365+ 366 + 365 = 1461\)
\( = 365+ 365+ 366 + 365 = 1461\)
(10) 15 ডিসেম্বর আমার জন্মদিন। 2013 সালে জন্মদিন ছিল রবিবার। 2014, 2015 ও 2016 সালে আমার জন্মদিন কী বার হিসাব করি।
15 ডিসেম্বর, 2013 রবিবার
15 ডিসেম্বর, 2013 সাল থেকে 15 ডিসেম্বর, 2014 পর্যন্ত মোট দিনসংখ্যা = 365
এখন,

\(\because \) ভাগশেষ = 1
\(\therefore\) রবিবার-এর পরে 1 দিন = সোমবার
\(\therefore\) 2014 সালে আমার জন্মদিন সোমবার ছিল।
15 ডিসেম্বর, 2014 থেকে 15 ডিসেম্বর, 2015 পর্যন্ত মোট দিনসংখ্যা = 365
এখন,

\(\because \) ভাগশেষ = 1
\(\therefore\) সোমবার-এর পরে 1 দিন = মঙ্গলবার
\(\therefore\) 2015 সালে আমার জন্মদিন মঙ্গলবার ছিল।
15 ডিসেম্বর, 2015 থেকে 15 ডিসেম্বর, 2016 পর্যন্ত মোট দিনসংখ্যা = 366
এখন,

\(\because \) ভাগশেষ = 2
\(\therefore\) মঙ্গলবার-এর পরে 2 দিন = বুধবার, বৃহস্পতিবার
\(\therefore\) 2016 সালে আমার জন্মদিন ছিল বৃহস্পতিবার।
15 ডিসেম্বর, 2013 সাল থেকে 15 ডিসেম্বর, 2014 পর্যন্ত মোট দিনসংখ্যা = 365
এখন,

\(\because \) ভাগশেষ = 1
\(\therefore\) রবিবার-এর পরে 1 দিন = সোমবার
\(\therefore\) 2014 সালে আমার জন্মদিন সোমবার ছিল।
15 ডিসেম্বর, 2014 থেকে 15 ডিসেম্বর, 2015 পর্যন্ত মোট দিনসংখ্যা = 365
এখন,

\(\because \) ভাগশেষ = 1
\(\therefore\) সোমবার-এর পরে 1 দিন = মঙ্গলবার
\(\therefore\) 2015 সালে আমার জন্মদিন মঙ্গলবার ছিল।
15 ডিসেম্বর, 2015 থেকে 15 ডিসেম্বর, 2016 পর্যন্ত মোট দিনসংখ্যা = 366
এখন,

\(\because \) ভাগশেষ = 2
\(\therefore\) মঙ্গলবার-এর পরে 2 দিন = বুধবার, বৃহস্পতিবার
\(\therefore\) 2016 সালে আমার জন্মদিন ছিল বৃহস্পতিবার।
(11) ভারতবর্ষ স্বাধীন হওয়ার পরে 2014 সাল পর্যন্ত লিপইয়ার কতগুলি সাল হয়েছে তা লিখি।
ভারতবর্ষ স্বাধীন হয়েছিল 15 আগস্ট 1947

\(\because \) 1947 সালটি 4 দ্বারা বিভাজ্য নয়,
\(\therefore\) 1947 লিপইয়ার নয়।
আবার

\(\because \) 1948 সালটি 4 দ্বারা বিভাজ্য
\(\therefore\) 1948 লিপইয়ার।
1948-এর পরে লিপইয়ারগুলি হল
\( 1948+4=1952,1952+4=1956,1956+4=1960,\)
\(1960+4=1964,1964+4=1968,1968+4=1972,\)
\(1972+4=1976,1976+4=1980,1980+4=1984,\)
\(1984+4=1988,1988+4=1992,1992+4=1996,\)
\(1996+4=2000,2000+4=2004,2004+4=2008,\)
\(2008+4=2012 \)
\(\therefore\) 1948 থেকে 2014 সাল পর্যন্ত মোট লিপইয়ার-এর সংখ্যা 17 টি ।

\(\because \) 1947 সালটি 4 দ্বারা বিভাজ্য নয়,
\(\therefore\) 1947 লিপইয়ার নয়।
আবার

\(\because \) 1948 সালটি 4 দ্বারা বিভাজ্য
\(\therefore\) 1948 লিপইয়ার।
1948-এর পরে লিপইয়ারগুলি হল
\( 1948+4=1952,1952+4=1956,1956+4=1960,\)
\(1960+4=1964,1964+4=1968,1968+4=1972,\)
\(1972+4=1976,1976+4=1980,1980+4=1984,\)
\(1984+4=1988,1988+4=1992,1992+4=1996,\)
\(1996+4=2000,2000+4=2004,2004+4=2008,\)
\(2008+4=2012 \)
\(\therefore\) 1948 থেকে 2014 সাল পর্যন্ত মোট লিপইয়ার-এর সংখ্যা 17 টি ।
WBBSE Class 6 Chapter 19.3 Math Solution in Bengali || Nije Kori 19.3 Class 6 || পশ্চিমবঙ্গ বোর্ডের ক্লাস Six অঙ্কের 19.3 অধ্যায়ের সমাধান || পশ্চিমবঙ্গ বোর্ডের ক্লাস সিক্সের অঙ্কের 19.3 অধ্যায়ের সমাধান
এই Page টি বা এই Website টির কোন প্রকার বিষয়বস্তু কপি করা বা সম্পাদনা করা নিষিদ্ধ। ভারতীয় Copywright আইন 1957 এর ধারা 63 অনুযায়ী, এই ফাইলটির সমস্ত অধিকার 'ছাত্র মিত্র Mathematics' অ্যাপ দ্বারা সংরক্ষিত। ছাত্র মিত্রের অনুমতি ছাড়া, এই Page টি বা এই Website টির কোন প্রকার বিষয়বস্তু কপি করা বা সম্পাদনা করা আইনত দন্ডনীয় অপরাধ। কেউ ছাত্র মিত্রের অনুমতি ছাড়া, এই Page টি বা এই Website টির কোন প্রকার বিষয়বস্তু কপি বা সম্পাদনা করলে ছাত্র মিত্র কতৃপক্ষ তার বিরুদ্ধে সকল প্রকার কঠোর আইনি পদক্ষেপ করবে।
West Bengal Board of Secondary Education Official Site
Class 8 : গণিত প্রভা (অষ্টম শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali.
Class 7 : গণিত প্রভা (সপ্তম শ্রেণি) বইয়ের সমস্ত সমাধান
www.wbresults.nic.in Official
Class 10 : মাধ্যমিক গণিত প্রকাশ (দশম শ্রেণি) বইয়ের সমস্ত সমাধান Class 10 Maths Solution WBBSE Bengali
Class 6 : গণিত প্রভা (ষষ্ঠ শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali
Class 9 : গণিত প্রকাশ (নবম শ্রেণি) বইয়ের সমাধান Maths Solution WBBSE Bengali
আজই Install করুন Chatra Mitra
Class 8 : গণিত প্রভা (অষ্টম শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali.
Class 7 : গণিত প্রভা (সপ্তম শ্রেণি) বইয়ের সমস্ত সমাধান
www.wbresults.nic.in Official
Class 10 : মাধ্যমিক গণিত প্রকাশ (দশম শ্রেণি) বইয়ের সমস্ত সমাধান Class 10 Maths Solution WBBSE Bengali
Class 6 : গণিত প্রভা (ষষ্ঠ শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali
Class 9 : গণিত প্রকাশ (নবম শ্রেণি) বইয়ের সমাধান Maths Solution WBBSE Bengali
আজই Install করুন Chatra Mitra



