কষে দেখি 22.1 ক্লাস 6 || পশ্চিমবঙ্গ বোর্ডের ক্লাস সিক্সের অঙ্কের 22.1 অধ্যায়ের সমাধান || WBBSE Class 6 Chapter 22.1 Math Solution in Bengali || West Bengal Board Class 6 Chapter 22.1 Math Solution || বিভিন্ন জ্যামিতিক চিত্র অঙ্কন|| Koshi dakhi 22.1 class 6 Wbbse || koshe dekhi 22.1 Class 6
Share this page using :
Koshi dakhi 22.1 class 6 Wbbse|| অনুপাত ও সমানুপাতের প্রাথমিক ধারণা || WBBSE Class 6 Chapter 22.1 Math Solution in Bengali || West Bengal Board Class 6 Chapter 22.1 Math Solution
কষে দেখি -22.1
Koshi dakhi 22.1 class 6 Wbbse|| অনুপাত ও সমানুপাতের প্রাথমিক ধারণা || WBBSE Class 6 Chapter 22.1 Math Solution in Bengali || West Bengal Board Class 6 Chapter 22.1 Math Solution
1. নীচের কোন্ কোন্ ক্ষেত্রে সরলরেখা দুটি পরস্পর লম্বভাবে আছে লেখার চেষ্টা করি।


পরস্পর লম্বভাবে আছে (b) ও (C)
2. শূন্যস্থান পূরণ করি :
(i) বিকেল 3টে বাজলে ঘড়ির ঘণ্টার কাঁটা ও মিনিটের কাঁটা
______ ভাবে থাকে।
লম্ব
(ii) পাড়ার সোজা ল্যাম্পপোস্টটা ভূমির সাথে ______ ভাবে
আছে।
লম্ব
3. আমি আমার দেখা দুটি জিনিসের নাম লিখি যারা পরস্পর লম্বভাবে আছে (নিজে করি)
(i) আমার ঘরের মেঝে, আমার পড়ার টেবিলের পায়ার সঙ্গে লম্বভাবে থাকে।
(ii) ফুটবল খেলার মাঠের সঙ্গে গোলপোস্টের দুটি খুঁটি লম্বভাবে থাকে।
(ii) ফুটবল খেলার মাঠের সঙ্গে গোলপোস্টের দুটি খুঁটি লম্বভাবে থাকে।
4. AB একটি সরলরেখাংশ আঁকি যার দৈর্ঘ্য 4 সেমি; এই AB সরলরেখাংশের। ওপর O একটি বিন্দু নিলাম যাতে \(AO = 1\) সেমি ও \(OB = 3\) সেমি. হয়। এবার O বিন্দুতে AB সরলরেখাংশের ওপর সেট স্কোয়ারের সাহায্যে MO লম্ব আঁকি।
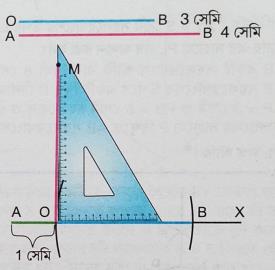
অঙ্কন পরিচিতি : AB সরলরেখাংশের O বিন্দুতে সেট স্কোয়ারের সাহায্যে MO লম্ব অঙ্কন করা হল যেখানে, AB = 4 সেমি, AO = 1 সেমি এবং BO = 3 সেমি।
5. PQ একটি সরলরেখাংশ আঁকি যার দৈর্ঘ্য 4 সেমি.। এই PQ সরলরেখাংশের উপর O একটি বিন্দু নিলাম। স্কেল ও পেনসিল কম্পাসের সাহায্যে O বিন্দুতে PQ সরলরেখাংশের উপর OM লম্ব আঁকি।


অঙ্কন পরিচিতি : \(PQ = 4\) সেমি সরলরেখাংশের উপর \(O\) বিন্দুতে \(OM\) লম্ব অঙ্কন করা হল।
6. \(XY\) একটি সরলরেখাংশ আঁকি যার দৈর্ঘ্য 5 সেমি.। এই \(XY\) সরলরেখাংশের বাইরে একটি বিন্দু P নিলাম। সেট স্কোয়ারের সাহায্যে P বিন্দু থেকে \(XY\) সরলরেখাংশের ওপর PL লম্ব আঁকি।


অঙ্কন পরিচিতি : \(XY = 5\) সেমি সরলরেখাংশের উপর \(L\) বিন্দুতে সেট স্কোয়ার-এর সাহায্যে \(PL\) লম্ব অঙ্কন করা হল।
7. AB একটি সরলরেখাংশ আঁকি যার দৈর্ঘ্য 8 সেমি.। এই AB সরলরেখাংশের উপরে একটি বিন্দু P নিলাম। যাতে \(AP = 3\) সেমি. ও \(PB = 5\) সেমি. হয়। স্কেল ও পেনসিল কম্পাসের সাহায্যে P বিন্দুতে AB সরলরেখাংশের উপর PL লম্ব আঁকি।


অঙ্কন পরিচিতি : AB সরলরেখাংশের উপর P বিন্দুতে PL লম্ব অঙ্কন করা হল যেখানে, AB = 8 সেমি, AP = 3 সেমি ও PB = 5 সেমি।
8. একটি সরলরেখাংশ AB অঙ্কন করি যার দৈর্ঘ্য 6 সেমি.। এই সরলরেখাংশের বাইরে একটি বিন্দু K নিই। স্কেল ও পেনসিল কম্পাসের সাহায্যে K বিন্দু থেকে AB সরলরেখাংশের উপর KL লম্ব আঁকি।


অঙ্কন পরিচিতি : AB সরলরেখাংশের বাইরে অবস্থিত একটি বিন্দু K থেকে AB-এর উপর লম্ব অঙ্কন করা হল যেখানে, AB = 6 সেমি।
9. স্কেল ও পেনসিলের সাহায্যে একটি ত্রিভুজ ABC আঁকি। এই ত্রিভুজের শীর্ষবিন্দু A, B ও C থেকে যথাক্রমে BC, AC ও AB বাহুর ওপরে যথাক্রমে তিনটি লম্ব AP, BQ ও CR আঁকি। দেখি AP, BQ ও CR সরলরেখাংশ তিনটি সমবিন্দু কিনা।

অঙ্কন পরিচিতি : \(\triangle \mathrm{ABC}\)-এর শীর্ষবিন্দু A, B ও C থেকে অঙ্কিত তিনটি লম্ব যথাক্রমে \(AP, BQ , CR\) পরস্পরকে O বিন্দুতে ছেদ করেছে। অর্থাৎ লম্ব তিনটি সমবিন্দু।
10. সেট স্কোয়ারের সাহায্যে ABC একটি সমকোণী ত্রিভুজ আঁকি যার। \(\angle ABC= 90^{\circ}\); B বিন্দু থেকে অতিভূজ AC-এর ওপর একটি লম্ব আঁকি। ত্রিভুজে A, B ও C বিন্দু থেকে বিপরীত বাহুগুলির উপর লম্ব তিনটি কোনো বিন্দুতে মিলিত হচ্ছে কিনা দেখি এবং কোনো বিন্দুতে মিলিত হলে সেই বিন্দুটির নাম লিখি।

অঙ্কন পরিচিতি : সেট স্কোয়ারের সাহায্যে অঙ্কিত সমকোণী ত্রিভুজ ABC-এর অতিভুজ AC-এর উপর BP লম্ব অঙ্কন করা হল।
AB ও BC বাহুদ্বয় পরস্পর লম্ব।
সুতরাং, আলাদা করে C বিন্দু ও A বিন্দু থেকে যথাক্রমে AB ও BC-এর উপর লম্ব অঙ্কন সম্ভব নয়।
\(\therefore\) লম্ব তিনটি একটি নির্দিষ্ট বিন্দু B-তে মিলিত হচ্ছে।
11. একটি সরলরেখার উপর একটি নির্দিষ্ট বিন্দুতে ______ টি লম্ব অঙ্কন করা যায়।
এক
12. একটি সরলরেখার বাইরের কোনো নির্দিষ্ট বিন্দু থেকে ওই
সরলরেখার উপর ______ (একটিই/একটির বেশি) লম্ব অঙ্কন করা যায়।
একটিই
13. একটি সরলরেখাংশ AB অঙ্কন করি। এই সরলরেখাংশের ওপর যে-কোনো দুটি বিন্দু P ও Q নিই। P ও Q বিন্দু দুটিতে AB সরলরেখাংশের উপর যথাক্রমে দুটি লম্ব PM ও QN আঁকি। দেখি PM ও QN সরলরেখাংশ দুটি পরস্পরছেদি না সমান্তরাল।

অঙ্কন পরিচিতি : AB সরলরেখাংশের উপরে P ও Q দুটি বিন্দুতে PM ও QN দুটি লম্ব। দেখা গেল, PM ও QN সরলরেখাংশ দুটি সমান্তরাল।
14. 4 সেমি. দৈর্ঘ্যের একটি সরলরেখাংশ অঙ্কন করি। ওই দৈর্ঘ্যের ব্যাসার্ধ নিয়ে একটি বৃত্ত আঁকি। বৃত্তের কেন্দ্রের নাম দিই O; ব্যাস ছাড়া স্কেল ও পেনসিলের সাহায্যে একটি জ্যা AB আঁকি। O বিন্দু থেকে AB জ্যা-এর ওপর একটি লম্ব OM আঁকি। AM ও BM সরলরেখাংশের দৈর্ঘ্য স্কেলের সাহায্যে মেপে AM ও BM সরলরেখাংশের সম্পর্ক লিখি।

অঙ্কন পরিচিতি : O-কে কেন্দ্র করে 4 সেমি ব্যাসার্ধবিশিষ্ট একটি বৃত্ত অঙ্কন করা হল যার AB জ্যা এবং OM হল AB-এর উপর অঙ্কিত লম্ব।
এখন স্কেলের সাহায্যে মেপে দেখা গেল, AM = BM জ্যামিতিক চিত্রটি থেকে সিদ্ধান্তে আসা যায় যে, বৃত্তের কেন্দ্র থেকে কোনো জ্যা-এর উপর লম্ব টানা হলে তা ওই জ্যা-কে সমদ্বিখণ্ডিত করে।
Koshi dakhi 22.1 class 6 Wbbse|| অনুপাত ও সমানুপাতের প্রাথমিক ধারণা || WBBSE Class 6 Chapter 22.1 Math Solution in Bengali || West Bengal Board Class 6 Chapter 22.1 Math Solution
এই Page টি বা এই Website টির কোন প্রকার বিষয়বস্তু কপি করা বা সম্পাদনা করা নিষিদ্ধ। ভারতীয় Copywright আইন 1957 এর ধারা 63 অনুযায়ী, এই ফাইলটির সমস্ত অধিকার 'ছাত্র মিত্র Mathematics' অ্যাপ দ্বারা সংরক্ষিত। ছাত্র মিত্রের অনুমতি ছাড়া, এই Page টি বা এই Website টির কোন প্রকার বিষয়বস্তু কপি করা বা সম্পাদনা করা আইনত দন্ডনীয় অপরাধ। কেউ ছাত্র মিত্রের অনুমতি ছাড়া, এই Page টি বা এই Website টির কোন প্রকার বিষয়বস্তু কপি বা সম্পাদনা করলে ছাত্র মিত্র কতৃপক্ষ তার বিরুদ্ধে সকল প্রকার কঠোর আইনি পদক্ষেপ করবে।
West Bengal Board of Secondary Education Official Site
Class 8 : গণিত প্রভা (অষ্টম শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali.
Class 7 : গণিত প্রভা (সপ্তম শ্রেণি) বইয়ের সমস্ত সমাধান
www.wbresults.nic.in Official
Class 10 : মাধ্যমিক গণিত প্রকাশ (দশম শ্রেণি) বইয়ের সমস্ত সমাধান Class 10 Maths Solution WBBSE Bengali
Class 6 : গণিত প্রভা (ষষ্ঠ শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali
Class 9 : গণিত প্রকাশ (নবম শ্রেণি) বইয়ের সমাধান Maths Solution WBBSE Bengali
আজই Install করুন Chatra Mitra
Class 8 : গণিত প্রভা (অষ্টম শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali.
Class 7 : গণিত প্রভা (সপ্তম শ্রেণি) বইয়ের সমস্ত সমাধান
www.wbresults.nic.in Official
Class 10 : মাধ্যমিক গণিত প্রকাশ (দশম শ্রেণি) বইয়ের সমস্ত সমাধান Class 10 Maths Solution WBBSE Bengali
Class 6 : গণিত প্রভা (ষষ্ঠ শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali
Class 9 : গণিত প্রকাশ (নবম শ্রেণি) বইয়ের সমাধান Maths Solution WBBSE Bengali
আজই Install করুন Chatra Mitra



