Koshi Dakhi 18.3 Class 6 || কষে দেখি 18.3 ক্লাস 6 || পশ্চিমবঙ্গ বোর্ডের ক্লাস সিক্সের অঙ্কের 18.3 অধ্যায়ের সমাধান|| Koshi dakhi 18.3 class 6 Wbbse || বর্গমূল অধ্যায়ের সমাধান|| WBBSE Class 6 Chapter 18.3 Math Solution in Bengali || West Bengal Board Class 6 Chapter 18.3 Math Solution
Share this page using :
পশ্চিমবঙ্গ বোর্ডের ক্লাস সিক্সের অঙ্কের 18.3 অধ্যায়ের সমাধান || Koshi Dakhi 18.3 Class 6 || কষে দেখি 18.3 ক্লাস 6 || Koshi dakhi 18.3 class 6 Wbbse Math Solution || বর্গমূল অধ্যায়ের সমাধান
কষে দেখি - 18.3
পশ্চিমবঙ্গ বোর্ডের ক্লাস সিক্সের অঙ্কের 18.3 অধ্যায়ের সমাধান || Koshi Dakhi 18.3 Class 6 || কষে দেখি 18.3 ক্লাস 6 || Koshi dakhi 18.3 class 6 Wbbse Math Solution || বর্গমূল অধ্যায়ের সমাধান
1. 1000-এর নিকটতম পূর্ণবর্গ সংখ্যা খুঁজি।

নির্ণেয় 1000-এর নিকটবর্তী পূর্ণবর্গ সংখ্যা \( =1000-39\)
\(=961=31^{2}\)
31-এর পরবর্তী পূর্ণসংখ্যা = 32
32-এর বর্গ \( =32 \times 32=1024 \)
এখানে \( (1024-1000)=24,1000-961=39 \)
\( \because 24<39 \)
\(\therefore\) 1000-এর নিকটতম পূর্ণবর্গ সংখ্যা = 1024
2. 9585 থেকে কোন্ ক্ষুদ্রতম সংখ্যা বিয়োগ করলে বিয়োগফল একটি পূর্ণবর্গ সংখ্যা হবে হিসাব করি।

\(\therefore\) নির্ণেয় ক্ষুদ্রতম সংখ্যা 176।
3. 5320-এর সাথে কোন্ ক্ষুদ্রতম সংখ্যা যোগ করলে যোগফল পূর্ণবর্গ সংখ্যা হবে হিসাব করি।

\( \therefore 5320-136=5184=72^{2} \)
\(72\)-এর পরবর্তী পূর্ণসংখ্যা \(= (72 + 1) = 73\)
\(\therefore 73\)-এর বর্গ \( =73^{2}=5329 \)
\(\therefore\) যে ক্ষুদ্রতম সংখ্যা যোগ করতে হবে তা হল \( (5329-5320)=9 \)
পশ্চিমবঙ্গ বোর্ডের ক্লাস সিক্সের অঙ্কের 18.3 অধ্যায়ের সমাধান || Koshi Dakhi 18.3 Class 6 || কষে দেখি 18.3 ক্লাস 6 || Koshi dakhi 18.3 class 6 Wbbse Math Solution || বর্গমূল অধ্যায়ের সমাধান
4. শুন্য ছাড়া এমন একটি ক্ষুদ্রতম পূর্ণবর্গ সংখ্যা খুঁজি যা 15, 25, 35 ও 45 দ্বারা বিভাজ্য।
15, 25, 35 ও 45 দ্বারা বিভাজ্য ক্ষুদ্রতম সংখ্যাটি হল ওই সংখ্যাগুলির লসাগু

\(\therefore\) 15, 25, 35, 45 দ্বারা বিভাজ্য ক্ষুদ্রতম সংখ্যাটি হল
\( =5 \times 5 \times 3 \times 3 \times 7\)
\(=5^{2} \times 3^{2} \times 7\)
\(=1575 \)
\(\because\) 1575-এর উৎপাদকগুলির মধ্যে 7 বিজোড় সংখ্যক বার আছে।
\(\therefore\) 15, 25, 35, 45 দ্বারা বিভাজ্য নির্ণেয় ক্ষুদ্রতম পূর্ণবর্গ সংখ্যা
\( =1575 \times 7\)
\(=11025 \)

\(\therefore\) 15, 25, 35, 45 দ্বারা বিভাজ্য ক্ষুদ্রতম সংখ্যাটি হল
\( =5 \times 5 \times 3 \times 3 \times 7\)
\(=5^{2} \times 3^{2} \times 7\)
\(=1575 \)
\(\because\) 1575-এর উৎপাদকগুলির মধ্যে 7 বিজোড় সংখ্যক বার আছে।
\(\therefore\) 15, 25, 35, 45 দ্বারা বিভাজ্য নির্ণেয় ক্ষুদ্রতম পূর্ণবর্গ সংখ্যা
\( =1575 \times 7\)
\(=11025 \)
5. চার অঙ্কের ক্ষুদ্রতম ও বৃহত্তম পূর্ণবর্গ সংখ্যা খুঁজি যা 8, 15, 20 ও 25 দিয়ে বিভাজ্য।
8, 15, 20 ও 25 দ্বারা বিভাজ্য ক্ষুদ্রতম সংখ্যাটি হল ওই সংখ্যাগুলির লসাগু

\(\therefore\) 8, 15, 20, 25 দ্বারা বিভাজ্য ক্ষুদ্রতম সংখ্যা
\( =2 \times 5 \times 2 \times 2 \times 3 \times 5\)
\(=2^{2} \times 5^{2} \times 2 \times 3\)
\(=600 \)
600-র উৎপাদকগুলির সঙ্গে 2 ও 3 বিজোড় সংখ্যক বার আছে।
\(\therefore\) 8, 15, 20, 25 দ্বারা বিভাজ্য নির্ণেয় ক্ষুদ্রতম পূর্ণবর্গ সংখ্যা
\( =600 \times 6=3600\)
3600-এর পরবর্তী পূর্ণবর্গ সংখ্যা \( =3600 \times 4=14400 \) যা পাঁচ অঙ্কের সংখ্যা।
\(\therefore\) 8, 15, 20 ও 25 দ্বারা বিভাজ্য চার অঙ্কের বৃহত্তম সংখ্যাটি 3600।

\(\therefore\) 8, 15, 20, 25 দ্বারা বিভাজ্য ক্ষুদ্রতম সংখ্যা
\( =2 \times 5 \times 2 \times 2 \times 3 \times 5\)
\(=2^{2} \times 5^{2} \times 2 \times 3\)
\(=600 \)
600-র উৎপাদকগুলির সঙ্গে 2 ও 3 বিজোড় সংখ্যক বার আছে।
\(\therefore\) 8, 15, 20, 25 দ্বারা বিভাজ্য নির্ণেয় ক্ষুদ্রতম পূর্ণবর্গ সংখ্যা
\( =600 \times 6=3600\)
3600-এর পরবর্তী পূর্ণবর্গ সংখ্যা \( =3600 \times 4=14400 \) যা পাঁচ অঙ্কের সংখ্যা।
\(\therefore\) 8, 15, 20 ও 25 দ্বারা বিভাজ্য চার অঙ্কের বৃহত্তম সংখ্যাটি 3600।
6. চার অঙ্কের ক্ষুদ্রতম পূর্ণবর্গ সংখ্যা খুঁজি।
চার অঙ্কের ক্ষুদ্রতম সংখ্যা = 1000

\( \therefore 31^{2}=1000-39=961 \), যা একটি তিন অঙ্কের সংখ্যা
\(\therefore\) 31-এর পরবর্তী পূর্ণসংখ্যা \( =32,32^{2}=1024 \)
\(\therefore\) চার অঙ্কের ক্ষুদ্রতম পূর্ণবর্গ সংখ্যা 1024।

\( \therefore 31^{2}=1000-39=961 \), যা একটি তিন অঙ্কের সংখ্যা
\(\therefore\) 31-এর পরবর্তী পূর্ণসংখ্যা \( =32,32^{2}=1024 \)
\(\therefore\) চার অঙ্কের ক্ষুদ্রতম পূর্ণবর্গ সংখ্যা 1024।
7. চার অঙ্কের বৃহত্তম পূর্ণবর্গ সংখ্যা খুঁজি।
চার অঙ্কের বৃহত্তম সংখ্যা হল = 9999

\(\therefore\) নির্ণেয় চার অঙ্কের বৃহত্তম পূর্ণবর্গ সংখ্যা
\( =9999-198\)
\(=9801 \)

\(\therefore\) নির্ণেয় চার অঙ্কের বৃহত্তম পূর্ণবর্গ সংখ্যা
\( =9999-198\)
\(=9801 \)
8. ভাগ পদ্ধতিতে নীচের সংখ্যার বর্গমূল খুঁজি।
(i) 256

\(\therefore\) নির্ণয় বর্গমূল = 16
(ii) 529

\(\therefore\) নির্ণেয় বর্গমূল = 23
(iii) 625

\(\therefore\) নির্ণেয় বর্গমূল = 25
(iv) 784
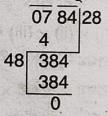
\(\therefore\) নির্ণেয় বর্গমূল = 28
(v) 1024

\(\therefore\) নির্ণেয় বর্গমূল = 32
(vi) 1225

\(\therefore\) নির্ণেয় বর্গমূল = 35
(vii) 961

\(\therefore\) নির্ণেয় বর্গমূল = 31
(viii) 841
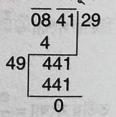
\(\therefore\) নির্ণেয় বর্গমূল = 29
(ix) 900

\(\therefore\) নির্ণেয় বর্গমূল = 30
(x) 1764

\(\therefore\) নির্ণেয় বর্গমূল = 42
9. বর্গমূল না করে নীচের সংখ্যাগুলির এককের ঘরের অঙ্ক কী কী হতে পারে তা লিখি এবং সংখ্যাগলির বর্গমূল কয় অঙ্কের সংখ্যা হবে তাও লিখি।
(a) 784
একক হতে পারে 2, 8, বর্গমূলের অঙ্ক সংখ্যা হবে 2টি
(b) 3676
একক হতে পারে 4, 6, বর্গমূলের অঙ্ক সংখ্যা হবে 2টি
(c) 160000
একক হতে পারে 0 বর্গমূলের অঙ্ক সংখ্যা হবে 3টি
(d) 1225
একক হতে পারে 5, বর্গমূলের অঙ্ক সংখ্যা হবে 2টি
(e) 2401
একক হতে পারে 1, 9, বর্গমূলের অঙ্ক সংখ্যা হবে 2টি
(f) 10201
(f) একক হতে পারে 1, 9, বর্গমূলের অঙ্ক সংখ্যা হবে 3টি
10. 5000-এর নিকটতম দুটি অখণ্ড পূর্ণবর্গ সংখ্যা খুঁজি।

5000-এর নিকটতম 5000 অপেক্ষা ছোটো পূর্ণবর্গ সংখ্যা
\( =(5000-100)=4900=70^{2} \)
70-এর পরবর্তী পূর্ণসংখ্যা = 71
\(\therefore\) 4900-এর পরবর্তী পূর্ণবর্গসংখ্যা \( =71 \times 71=5041 \)
\(\therefore\) 5000-এর নিকটতম দুটি অখণ্ড পূর্ণবর্গ সংখ্যা = 4900, 5041
11. দুটি ধনাত্মক পূর্ণসংখ্যার গুণফল 1576 এবং ভাগফল \(\frac{9}{7}\); সংখ্যাগুলি কী হবে হিসাব করি।
প্রশ্নানুসারে, প্রথম সংখ্যা \( \times \) দ্বিতীয় সংখ্যা = 1575
এবং \(\frac{\text{প্রথম সংখ্যা}}{\text{দ্বিতীয় সংখ্যা}}\) \( =\frac{9}{7} \) [ধরি, প্রথম সংখ্যা > দ্বিতীয় সংখ্যা]
\(\therefore\) প্রথম সংখ্যা \( \times \) দ্বিতীয় সংখ্যা \(\times \frac{\text{প্রথম সংখ্যা}}{\text{দ্বিতীয় সংখ্যা}} = 1575 \times \frac{9}{7} \)
প্রথম সংখ্যা\(^2\) \( =225 \times 9 \)
প্রথম সংখ্যা \( =\sqrt{225 \times 9}\)
\(=\sqrt{15 \times 15 \times 3 \times 3} \)
\( =15 \times 3\)
\(=45 \)
\(\because\) প্রথম সংখ্যা \( \times \) দ্বিতীয় সংখ্যা = 1575
বা, \(45 \times \) দ্বিতীয় সংখ্যা = 1575
বা, দ্বিতীয় সংখ্যা \( =\frac{1575}{45}=35 \)
\(\therefore\) দ্বিতীয় সংখ্যা = 35
\(\therefore\) সংখ্যা দুটি হল 45 ও 35।
এবং \(\frac{\text{প্রথম সংখ্যা}}{\text{দ্বিতীয় সংখ্যা}}\) \( =\frac{9}{7} \) [ধরি, প্রথম সংখ্যা > দ্বিতীয় সংখ্যা]
\(\therefore\) প্রথম সংখ্যা \( \times \) দ্বিতীয় সংখ্যা \(\times \frac{\text{প্রথম সংখ্যা}}{\text{দ্বিতীয় সংখ্যা}} = 1575 \times \frac{9}{7} \)
প্রথম সংখ্যা\(^2\) \( =225 \times 9 \)
প্রথম সংখ্যা \( =\sqrt{225 \times 9}\)
\(=\sqrt{15 \times 15 \times 3 \times 3} \)
\( =15 \times 3\)
\(=45 \)
\(\because\) প্রথম সংখ্যা \( \times \) দ্বিতীয় সংখ্যা = 1575
বা, \(45 \times \) দ্বিতীয় সংখ্যা = 1575
বা, দ্বিতীয় সংখ্যা \( =\frac{1575}{45}=35 \)
\(\therefore\) দ্বিতীয় সংখ্যা = 35
\(\therefore\) সংখ্যা দুটি হল 45 ও 35।
12. 202*-এর * অঙ্কটি কী হলে সংখ্যাটি পূর্ণবর্গ হবে তা হিসাব করি।

[\(\because\) 202★-কে পূর্ণবর্গ হতে হবে]
\(\therefore\) 202★ -এর ‘★’ অঙ্কটি 5 হলে সংখ্যাটি পূর্ণবর্গ হবে।
পশ্চিমবঙ্গ বোর্ডের ক্লাস সিক্সের অঙ্কের 18.3 অধ্যায়ের সমাধান || Koshi Dakhi 18.3 Class 6 || কষে দেখি 18.3 ক্লাস 6 || Koshi dakhi 18.3 class 6 Wbbse Math Solution || বর্গমূল অধ্যায়ের সমাধান
এই Page টি বা এই Website টির কোন প্রকার বিষয়বস্তু কপি করা বা সম্পাদনা করা নিষিদ্ধ। ভারতীয় Copywright আইন 1957 এর ধারা 63 অনুযায়ী, এই ফাইলটির সমস্ত অধিকার 'ছাত্র মিত্র Mathematics' অ্যাপ দ্বারা সংরক্ষিত। ছাত্র মিত্রের অনুমতি ছাড়া, এই Page টি বা এই Website টির কোন প্রকার বিষয়বস্তু কপি করা বা সম্পাদনা করা আইনত দন্ডনীয় অপরাধ। কেউ ছাত্র মিত্রের অনুমতি ছাড়া, এই Page টি বা এই Website টির কোন প্রকার বিষয়বস্তু কপি বা সম্পাদনা করলে ছাত্র মিত্র কতৃপক্ষ তার বিরুদ্ধে সকল প্রকার কঠোর আইনি পদক্ষেপ করবে।
West Bengal Board of Secondary Education Official Site
Class 8 : গণিত প্রভা (অষ্টম শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali.
Class 7 : গণিত প্রভা (সপ্তম শ্রেণি) বইয়ের সমস্ত সমাধান
www.wbresults.nic.in Official
Class 10 : মাধ্যমিক গণিত প্রকাশ (দশম শ্রেণি) বইয়ের সমস্ত সমাধান Class 10 Maths Solution WBBSE Bengali
Class 6 : গণিত প্রভা (ষষ্ঠ শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali
Class 9 : গণিত প্রকাশ (নবম শ্রেণি) বইয়ের সমাধান Maths Solution WBBSE Bengali
আজই Install করুন Chatra Mitra
Class 8 : গণিত প্রভা (অষ্টম শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali.
Class 7 : গণিত প্রভা (সপ্তম শ্রেণি) বইয়ের সমস্ত সমাধান
www.wbresults.nic.in Official
Class 10 : মাধ্যমিক গণিত প্রকাশ (দশম শ্রেণি) বইয়ের সমস্ত সমাধান Class 10 Maths Solution WBBSE Bengali
Class 6 : গণিত প্রভা (ষষ্ঠ শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali
Class 9 : গণিত প্রকাশ (নবম শ্রেণি) বইয়ের সমাধান Maths Solution WBBSE Bengali
আজই Install করুন Chatra Mitra



