Koshi Dakhi 12 Class 6 Math Solution || কষে দেখি 12 ক্লাস 6 || গণিতপ্রভা তিনটি সংখ্যার গ.সা.গু ও ল.সা.গু || WBBSE Class 6 Chapter 10 Math Solution in Bengali || West Bengal Board Class 6 Chapter 12 Math Solution || পশ্চিমবঙ্গ বোর্ডের ক্লাস সিক্সের অঙ্কের 12অধ্যায়ের সমাধান
Share this page using :
Koshi Dakhi 12 Class 6 Math Solution || কষে দেখি 12 ক্লাস 6 || তিনটি সংখ্যার গ.সা.গু ও ল.সা.গু
কষে দেখি - 12
Koshi Dakhi 12 Class 6 Math Solution || কষে দেখি 12 ক্লাস 6 || তিনটি সংখ্যার গ.সা.গু ও ল.সা.গু
1. তিনটি ছোটো ট্যাঙ্কে যথাক্রমে 35 লিটার, 56 লিটার ও 84 লিটার তেল আছে। হিসেব করি সবচেয়ে বড়ো কত মাপের পাত্র দিয়ে ট্যাংক তিনটির তেল পূর্ণসংখ্যক বার মাপতে পারব।
তিনটি ছোটো ট্যাঙ্কে তেল ধরে 35 লিটার, 56 লিটার ও 84 লিটার।
সবচেয়ে বড়ো মাপের পাত্রটির আয়তন হবে 35 লিটার, 56 লিটার ও 84 লিটার-এর গসাগু।
\(\therefore\) 35, 56, 84-এর গসাগু = 7

\(\therefore\) সবচেয়ে বড়ো মাপের পাত্রটি হবে 7 লিটারের।
সবচেয়ে বড়ো মাপের পাত্রটির আয়তন হবে 35 লিটার, 56 লিটার ও 84 লিটার-এর গসাগু।
\(\therefore\) 35, 56, 84-এর গসাগু = 7

\(\therefore\) সবচেয়ে বড়ো মাপের পাত্রটি হবে 7 লিটারের।
2. আমাদের স্কুলের হলঘরের দৈর্ঘ্য 2000 সেমি. এবং প্রস্থ 1600 সেমি.। হিসেব করে দেখি সবচেয়ে লম্বা কত দৈর্ঘ্যের ফিতে দিয়ে এই হল ঘরের দৈর্ঘ্য ও প্রস্থ দু-দিকই পূর্ণসংখ্যায় মাপতে পারব।
হলঘরের দৈর্ঘ্য 2000 সেমি ও প্রস্থ 1600 সেমি
সবচেয়ে বড়ো মাপের ফিতের দৈর্ঘ্য হবে 2000 সেমি এবং 1600 সেমি-এর গসাগু।

\(\therefore\) 2000, 1600-এর গসাগু \(=5 \times 5 \times 2 \times 2 \times 2 \times 2=400 \)
\(\therefore\) নির্ণেয় সবচেয়ে বড়ো মাপের ফিতার দৈর্ঘ্য = 400 সেমি = 4 মিটার
সবচেয়ে বড়ো মাপের ফিতের দৈর্ঘ্য হবে 2000 সেমি এবং 1600 সেমি-এর গসাগু।

\(\therefore\) 2000, 1600-এর গসাগু \(=5 \times 5 \times 2 \times 2 \times 2 \times 2=400 \)
\(\therefore\) নির্ণেয় সবচেয়ে বড়ো মাপের ফিতার দৈর্ঘ্য = 400 সেমি = 4 মিটার
3. 1071টি ধুতি, 595টি শাড়ি ও 357টি জামা মজুত আছে। হিসেব করে দেখি সবচেয়ে বেশি কত পরিবারের মধ্যে ওই জিনিসগুলি সমানভাগে ভাগ করে দিতে পারব এবং প্রত্যেক পরিবার কতগুলি করে কী কী জিনিস পাবে।
সবচেয়ে বেশি কটি পরিবার ধুতি, শাড়ি ও জামা সমানভাবে পাবে তা জানতে হলে 1071, 595, 357-এর গসাগু নির্ণয় করতে হবে

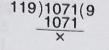
\(\therefore\) নির্ণেয় সবচেয়ে বেশি পরিবার সংখ্যা = 119 টি
এখন, প্রত্যেক পরিবার ধুতি পাবে \((1071 \div 119 )\) টি = 9 টি
শাড়ি পাবে \((595 \div 119) \) টি = 5 টি
জামা পাবে \((357 \div 119)\) টি = 3 টি

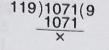
\(\therefore\) নির্ণেয় সবচেয়ে বেশি পরিবার সংখ্যা = 119 টি
এখন, প্রত্যেক পরিবার ধুতি পাবে \((1071 \div 119 )\) টি = 9 টি
শাড়ি পাবে \((595 \div 119) \) টি = 5 টি
জামা পাবে \((357 \div 119)\) টি = 3 টি
4. একটি ইঞ্জিনের সামনের চাকার পরিধি 1 মি. 4 ডেসিমি. এবং পেছনের চাকার পরিধি সামনের চাকার পরিধির আড়াই গুণ। হিসেব করে দেখি কমপক্ষে কত পথ গেলে চাকা একই সঙ্গে পূর্ণসংখ্যক বার ঘোরা সম্পূর্ণ করবে।
ইঞ্জিনের সামনের চাকার পরিধি = 1 মি 4 ডেসিমি = 14 ডেসিমি
ইঞ্জিনের পিছনের চাকার পরিধি
\( =14 \times 2 \frac{1}{2} \) ডেসিমি
\( =\left(14 \times \frac{5}{2}\right) \) ডেসিমি
= 35 ডেসিমি
কমপক্ষে যত পথ গেলে চাকা দুটি একইসঙ্গে পূর্ণসংখ্যক বার আবর্তন করবে তা হল 14 ডেসিমি ও 35 ডেসিমি-এর লসাগু।

\(\therefore\) নির্ণেয় লসাগু \( =7 \times 2 \times 5=70 \)
\(\therefore\) 14 ডেসিমি ও 35 ডেসিমি-এর লসাগু = 70 ডেসিমি = 7 মিটার
\(\therefore\) কমপক্ষে 7 মিটার পথ গেলে চাকা দুটি একইসঙ্গে পূর্ণসংখ্যক বার ঘোরা সম্পূর্ণ করবে।
ইঞ্জিনের পিছনের চাকার পরিধি
\( =14 \times 2 \frac{1}{2} \) ডেসিমি
\( =\left(14 \times \frac{5}{2}\right) \) ডেসিমি
= 35 ডেসিমি
কমপক্ষে যত পথ গেলে চাকা দুটি একইসঙ্গে পূর্ণসংখ্যক বার আবর্তন করবে তা হল 14 ডেসিমি ও 35 ডেসিমি-এর লসাগু।

\(\therefore\) নির্ণেয় লসাগু \( =7 \times 2 \times 5=70 \)
\(\therefore\) 14 ডেসিমি ও 35 ডেসিমি-এর লসাগু = 70 ডেসিমি = 7 মিটার
\(\therefore\) কমপক্ষে 7 মিটার পথ গেলে চাকা দুটি একইসঙ্গে পূর্ণসংখ্যক বার ঘোরা সম্পূর্ণ করবে।
5. নীচের সংখ্যাগুলির গ.সা.গু.-এর মান কী হবে খুঁজি।
(a) 24,36,54

\(\therefore\) নির্ণেয় গ.সা.গু. \(=2 \times 3= 6\)
(b) 24,30,40,48

\(\therefore\) নির্ণেয় গ.সা.গু. = 2
Koshi Dakhi 12 Class 6 Math Solution || কষে দেখি 12 ক্লাস 6 || তিনটি সংখ্যার গ.সা.গু ও ল.সা.গু
(c) 296,703,814

\(\therefore\) নির্ণেয় গ.সা.গু. = 37
(d) 160,165,305

\(\therefore\) নির্ণেয় গ.সা.গু. = 5
(e) 165,264,286

\(\therefore\) নির্ণেয় গ.সা.গু. = 11
(f) 906, 1510, 1057
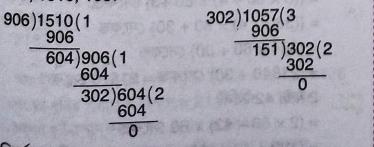
\(\therefore\) নির্ণেয় গ.সা.গু. = 151
6. কোন্ বৃহত্তম সংখ্যা দিয়ে 306, 810 ও 2214-কে ভাগ করলে প্রতিক্ষেত্রে কোনো ভাগশেষ থাকবে না তা হিসেব করে দেখি।
যে বৃহত্তম সংখ্যা দিয়ে 306, 810, 2214-কে ভাগ করলে কোনো ভাগশেষ থাকবে না তা হল 306, 810 ও 2214-এর গসাগু

\(\therefore\) নির্ণেয় বৃহত্তম সংখ্যা হল 18, যা দিয়ে 306, 810 ও 2214-কে ভাগ করলে কোনো ভাগশেষ থাকবে না।

\(\therefore\) নির্ণেয় বৃহত্তম সংখ্যা হল 18, যা দিয়ে 306, 810 ও 2214-কে ভাগ করলে কোনো ভাগশেষ থাকবে না।
Koshi Dakhi 12 Class 6 || কষে দেখি 12 ক্লাস 6 || তিনটি সংখ্যার গ.সা.গু ও ল.সা.গু
7. তিনটি আলাদা আলাদা রাস্তার ক্রসিংয়ে তিনটি ট্রাফিক সিগন্যালের আলো যথাক্রমে প্রতি 16 সেকেন্ড, 28 সেকেন্ড ও 40 সেকেন্ড অন্তর পরিবর্তন হয়। যদি সকাল 8 টায় একসাথে আলোর পরিবর্তন করে তাহলে হিসেব করে দেখি আবার কখন ওই তিনটি ট্রাফিক সিগন্যালের আলো একসাথে আবার পরিবর্তন করবে।
একসঙ্গে তিনটি ট্রাফিক সিগন্যালের আলো আবার কখন পরিবর্তিত হবে তা জানতে হলে 16 সেকেন্ড, 28 সেকেন্ড ও 40 সেকেন্ড-এর লসাগু নির্ণয় করতে হবে।

\(\therefore\) নির্ণেয় লসাগু \( =2 \times 2 \times 2 \times 2 \times 7 \times 5=560 \)
16 সেকেন্ড, 28 সেকেন্ড ও 40 সেকেন্ডের লসাগু 560 সেকেন্ড 560 সেকেন্ড
\(\therefore\) 560 সেকেন্ড \( =(560 \div 60) \) মিনিট

= 9 মিনিট 20 সেকেন্ড
\(\therefore\) সকাল 8 টা থেকে 9 মিনিট 20 সেকেন্ড পরে অর্থাৎ, সকাল 8টা 9 মিনিট 20 সেকেন্ডে আবার একসঙ্গে ট্রাফিক সিগন্যালের আলোগুলি পরিবর্তিত হবে।

\(\therefore\) নির্ণেয় লসাগু \( =2 \times 2 \times 2 \times 2 \times 7 \times 5=560 \)
16 সেকেন্ড, 28 সেকেন্ড ও 40 সেকেন্ডের লসাগু 560 সেকেন্ড 560 সেকেন্ড
\(\therefore\) 560 সেকেন্ড \( =(560 \div 60) \) মিনিট

= 9 মিনিট 20 সেকেন্ড
\(\therefore\) সকাল 8 টা থেকে 9 মিনিট 20 সেকেন্ড পরে অর্থাৎ, সকাল 8টা 9 মিনিট 20 সেকেন্ডে আবার একসঙ্গে ট্রাফিক সিগন্যালের আলোগুলি পরিবর্তিত হবে।
8. আমাদের বাড়িতে তিনটি লাঠি আছে যাদের দৈর্ঘ্য যথাক্রমে 45 সেমি., 50 সেমি., 75 সেমি.। হিসেব করে দেখি এই তিনটি লাঠির প্রত্যেকটি দিয়ে কমপক্ষে কত দৈর্ঘ্যের ফিতে সম্পূর্ণভাবে মাপতে পারব।
লাঠিগুলি দিয়ে কমপক্ষে যে দৈর্ঘ্যর ফিতে সম্পূর্ণভাবে মাপা যাবে তা নির্ণয় করতে হলে 45 সেমি, 50 সেমি, ও 75 সেমি-এর লসাগু নির্ণয় করতে হবে।
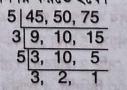
\(\therefore\) লসাগু \( =5 \times 3 \times 5 \times 3 \times 2=450 \)
\(\therefore\) 45 সেমি, 50 সেমি ও 75 সেমির লসাগু 450 সেমি।
\(\therefore\) কমপক্ষে 450 সেমি দৈর্ঘ্যের ফিতে 45 সেমি, 50 সেমি, 75 সেমি দৈর্ঘ্যের লাঠি দিয়ে মাপা যাবে।

\(\therefore\) লসাগু \( =5 \times 3 \times 5 \times 3 \times 2=450 \)
\(\therefore\) 45 সেমি, 50 সেমি ও 75 সেমির লসাগু 450 সেমি।
\(\therefore\) কমপক্ষে 450 সেমি দৈর্ঘ্যের ফিতে 45 সেমি, 50 সেমি, 75 সেমি দৈর্ঘ্যের লাঠি দিয়ে মাপা যাবে।
9. ক্ষুদ্রতম সংখ্যা খুঁজি যা 15, 20, 24 এবং 32 দ্বারা বিভাজ্য।
15, 20, 24 এবং 32 দ্বারা বিভাজ্য ক্ষুদ্রতম সংখ্যাটি হবে ওই সংখ্যাগুলির লসাগু।

\(\therefore\) নির্ণেয় ক্ষুদ্রতম সংখ্যা \( =3 \times 5 \times 2 \times 2 \times 2 \times 4=480 \)

\(\therefore\) নির্ণেয় ক্ষুদ্রতম সংখ্যা \( =3 \times 5 \times 2 \times 2 \times 2 \times 4=480 \)
10. নীচের সংখ্যাগুলির ল.সা.গু.-এর মান খুঁজি।
(a) 36, 60, 72
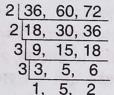
\(\therefore\) নির্ণেয় ল.সা.গু. \(=2 \times 2 \times 3 \times 3 \times 5 \times 2\) = 360
(b) 24, 36, 45, 60

\(\therefore\) নির্ণেয় ল.সা.গু. \(=2 \times 2 \times 3 \times 3 \times 5 \times 2=360\)
(c) 105, 119, 289

\(\therefore\) নির্ণেয় ল.সা.গু. \(=7 \times 17 \times 15 \times 17= 30345\)
Koshi Dakhi 12 Class 6 Math Solution || কষে দেখি 12 ক্লাস 6 || তিনটি সংখ্যার গ.সা.গু ও ল.সা.গু
(d) 144, 180, 348

\(\therefore\) নির্ণেয় ল.সা.গু. \(=2 \times 2 \times 3 \times 3 \times 4 \times 5 \times 29 = 20880\)
(e) 110, 165, 330

\(\therefore\) নির্ণেয় ল.সা.গু. \(=5 \times 11 \times 2 \times 3 = 330\)
(f) 204, 408, 306

\(\therefore\) নির্ণেয় ল.সা.গু. \(=2 \times 2 \times 3 \times 17 \times 2 \times 3 = 1224\)
Koshi Dakhi 12 Class 6 Math Solution || কষে দেখি 12 ক্লাস 6 || তিনটি সংখ্যার গ.সা.গু ও ল.সা.গু
11. নীচের রাশিগুলির ল.সা.গু. ও গ.সা.গু.-এর মান খুঁজি।
(a) 6 টাকা 50 পয়সা, 5 টাকা 20 পয়সা এবং 7 টাকা 80 পয়সা।
6 টাকা 50 পয়সা = 650 পয়সা,
5 টাকা 20 পয়সা = 520 পয়সা,
7 টাকা 80 পয়সা = 780 পয়সা

\(\therefore\) নির্ণেয় গ.সা.গু. \(=2 \times 5 \times 13=130\)
\(\therefore\) 650 পয়সা, 520 পয়সা ও 780 পয়সার গসাগু
= 130 পয়সা = 1 টাকা 30 পয়সা
নির্ণেয় লসাগু \( =2 \times 5 \times 13 \times 2 \times 5 \times 2 \times 3=7800 \)
\(\therefore\) 650 পয়সা, 520 পয়সা ও 780 পয়সার লসাগু
= 7800 পয়সা = 78 টাকা
5 টাকা 20 পয়সা = 520 পয়সা,
7 টাকা 80 পয়সা = 780 পয়সা

\(\therefore\) নির্ণেয় গ.সা.গু. \(=2 \times 5 \times 13=130\)
\(\therefore\) 650 পয়সা, 520 পয়সা ও 780 পয়সার গসাগু
= 130 পয়সা = 1 টাকা 30 পয়সা
নির্ণেয় লসাগু \( =2 \times 5 \times 13 \times 2 \times 5 \times 2 \times 3=7800 \)
\(\therefore\) 650 পয়সা, 520 পয়সা ও 780 পয়সার লসাগু
= 7800 পয়সা = 78 টাকা
(b) 2 মি. 28 সেমি., 3 মি. 42 সেমি., 4 মি. 56 সেমি.।
2 মিটার 28 সেমি = 228 সেমি
3 মিটার 42 সেমি = 342 সেমি
4 মিটার 56 সেমি = 456 সেমি

\(\therefore\) নির্ণেয় গসাগু \( =2 \times 19 \times 3=114 \)
\(\therefore\) 228 সেমি, 342 সেমি ও 456 সেমি-এর গসাগু
= 1368 সেমি = 13 মিটার 68 সেমি
3 মিটার 42 সেমি = 342 সেমি
4 মিটার 56 সেমি = 456 সেমি

\(\therefore\) নির্ণেয় গসাগু \( =2 \times 19 \times 3=114 \)
\(\therefore\) 228 সেমি, 342 সেমি ও 456 সেমি-এর গসাগু
= 1368 সেমি = 13 মিটার 68 সেমি
(c) 3 লি. 600 মিলিলি., 4 লি. 800 মিলিলি. এবং 6 লি.।
3 লিটার 600 মিলিলি = 3600 মিলিলি
4 লিটার 800 মিলিলি = 4800 মিলিলি
6 লিটার = 6000 মিলিলি

\(\therefore\) নির্ণেয় গসাগু \( =2 \times 2 \times 2 \times 2 \times 5 \times 5 \times 3=1200 \)
\(\therefore\) 3600 মিলিলি, 4800 মিলিলি ও 6000 মিলিলি-এর গসাগু
= 1200 মিলিলি = 1 লিটার 200 মিলি
\(\therefore\) নির্ণেয় লসাগু \( =2 \times 2 \times 2 \times 2 \times 5 \times 5 \times 3 \times 3 \times 4 \times 5 \)
= 72000 মিলিলি
\(\therefore\) 3600 মিলিলি, 4800 মিলিলি ও 600 মিলিলি-এর লসাগু
= 72000 মিলিলি = 72 লিটার
4 লিটার 800 মিলিলি = 4800 মিলিলি
6 লিটার = 6000 মিলিলি

\(\therefore\) নির্ণেয় গসাগু \( =2 \times 2 \times 2 \times 2 \times 5 \times 5 \times 3=1200 \)
\(\therefore\) 3600 মিলিলি, 4800 মিলিলি ও 6000 মিলিলি-এর গসাগু
= 1200 মিলিলি = 1 লিটার 200 মিলি
\(\therefore\) নির্ণেয় লসাগু \( =2 \times 2 \times 2 \times 2 \times 5 \times 5 \times 3 \times 3 \times 4 \times 5 \)
= 72000 মিলিলি
\(\therefore\) 3600 মিলিলি, 4800 মিলিলি ও 600 মিলিলি-এর লসাগু
= 72000 মিলিলি = 72 লিটার
Koshi Dakhi 12 Class 6 Math Solution || কষে দেখি 12 ক্লাস 6 || তিনটি সংখ্যার গ.সা.গু ও ল.সা.গু
(d) 6 ঘণ্টা 4 মিনিট 30 সেকেন্ড, 2 ঘণ্টা 42 মিনিট।
6 ঘণ্টা 4 মিনিট 30 সেকেন্ড
\( =\{(6 \times 60+4) \times 60+3\} \) সেকেন্ড
\( =\{(360+4) \times 60+30\} \) সেকেন্ড
\( =\{364 \times 60+30\} \) সেকেন্ড
\(= (21840 + 30)\) সেকেন্ড
= 21870 সেকেন্ড
2 ঘণ্টা 42 মিনিট
\(= (2 \times 60 + 42) \times 60\) সেকেন্ড
\(= (120 + 42) \times 60 = 162\times 60 = 9720\) সেকেন্ড

\(\therefore\) নির্ণেয় গসাগু \( =2 \times 5 \times 3 \times 3 \times 3 \times 3 \times 3=2430 \)
\(\therefore\) নির্ণেয় লসাগু
\( =2 \times 5 \times 3 \times 3 \times 3 \times 3 \times 3 \times 9 \times 4=87480 \)
2430 সেকেন্ড \(= 2430\div 60\) মিনিট

87480 সেকেন্ড \(= 87480\div 60\) মিনিট

1458 মিনিট \(= 1458\div 60\) ঘণ্টা

\(\therefore\) 21870 সেকেন্ড ও 9720 সেকেন্ডের গসাগু
= 2430 সেকেন্ড = 40 মিনিট 30 সেকেন্ড
\(\therefore\) 21870 সেকেন্ড ও 9720 সেকেন্ড-এর লসাগু
= 87480 সেকেন্ড = 24 ঘণ্টা 18 মিনিট
\( =\{(6 \times 60+4) \times 60+3\} \) সেকেন্ড
\( =\{(360+4) \times 60+30\} \) সেকেন্ড
\( =\{364 \times 60+30\} \) সেকেন্ড
\(= (21840 + 30)\) সেকেন্ড
= 21870 সেকেন্ড
2 ঘণ্টা 42 মিনিট
\(= (2 \times 60 + 42) \times 60\) সেকেন্ড
\(= (120 + 42) \times 60 = 162\times 60 = 9720\) সেকেন্ড

\(\therefore\) নির্ণেয় গসাগু \( =2 \times 5 \times 3 \times 3 \times 3 \times 3 \times 3=2430 \)
\(\therefore\) নির্ণেয় লসাগু
\( =2 \times 5 \times 3 \times 3 \times 3 \times 3 \times 3 \times 9 \times 4=87480 \)
2430 সেকেন্ড \(= 2430\div 60\) মিনিট

87480 সেকেন্ড \(= 87480\div 60\) মিনিট

1458 মিনিট \(= 1458\div 60\) ঘণ্টা

\(\therefore\) 21870 সেকেন্ড ও 9720 সেকেন্ডের গসাগু
= 2430 সেকেন্ড = 40 মিনিট 30 সেকেন্ড
\(\therefore\) 21870 সেকেন্ড ও 9720 সেকেন্ড-এর লসাগু
= 87480 সেকেন্ড = 24 ঘণ্টা 18 মিনিট
12. নীচের সংখ্যাজোড়াগুলির ক্ষেত্রে যাচাই করি যে, সংখ্যাদুটির গুণফল তাদের ল.সা.গু ও গ.সা.গু.-এর গুণফলের সমান কিনা।
(a) 87, 145

গ.সা.গু. = 29, ল.সা.গু. \(=29 \times 3 \times 5 = 435\)
সংখ্যা দুটির গ.সা.গু. \(\times\) ল.সা.গু. \(=29\times435=12615\)
সংখ্যা দুটির গুণফল \(=87 \times 145=12615\)
\(\therefore\) সংখ্যা দুটির গুণফল = সংখ্যা দুটির গ.সা.গু. \(\times\) ল.সা.গু.
(b) 60, 75

গ.সা.গু. \(= 5\times3=15\), ল.সা.গু. \( =5\times3\times5\times4= 300\)
সংখ্যাদুটির গ.সা.গু. \(\times\) ল.সা.গু. \(=15 \times 300 = 4500\)
সংখ্যা দুটির গুণফল \(=60 \times 75 = 4500\)
\(\therefore\) সংখ্যা দুটির গুণফল = সংখ্যা দুটির গ.সা.গু. \(\times\) ল.সা.গু.
Koshi Dakhi 12 Class 6 Math Solution || কষে দেখি 12 ক্লাস 6 || তিনটি সংখ্যার গ.সা.গু ও ল.সা.গু
(c) 42, 63

গ.সা.গু. \(=7 \times 3= 21\), ল.সা.গু. \(=7 \times 3 \times 2 \times 3= 126\)
সংখ্যা দুটির গ.সা.গু. \(\times\) ল.সা.গু. \(=21 \times 126 = 2646\)
সংখ্যা দুটির গুণফল \(=42 \times 63 = 2646\)
\(\therefore\) সংখ্যা দুটির গুণফল = সংখ্যা দুটির গ.সা.গু. \(\times\) ল.সা.গু.
(d) 186, 403

গ.সা.গু. \(= 31\), ল.সা.গু. \(= 31 \times 6 \times 13 = 2418 \)
সংখ্যা দুটির গ.সা.গু. \(\times\) ল.সা.গু. \( =31 \times 2418=74958 \)
সংখ্যা দুটির গুণফল \( =186 \times 403=74958 \)
\(\therefore\) সংখ্যা দুটির গুণফল = সংখ্যা দুটির গ.সা.গু \(\times\) ল.সা.গু.
13. দুটি সংখ্যার ল.সা.গু ও গ.সা.গু. যথাক্রমে 2175 এবং 145; যদি একটি সংখ্যা 725 হয়, তাহলে অপর সংখ্যাটি কত হবে হিসেব করি।
একটি সংখ্যা \( \times \) অপর সংখ্যা = সংখ্যাদ্বয়ের লসাগু \( \times \) গসাগু
বা, \( 725 \times \) অপর সংখ্যা \(= 2175 \times 145\)
বা, অপর সংখ্যা \( =\frac{2175 \times 145}{725}=435 \)
\(\therefore\) নির্ণেয় অপর সংখ্যা \(= 435\)
বা, \( 725 \times \) অপর সংখ্যা \(= 2175 \times 145\)
বা, অপর সংখ্যা \( =\frac{2175 \times 145}{725}=435 \)
\(\therefore\) নির্ণেয় অপর সংখ্যা \(= 435\)
14. 145 ও 232 সংখ্যা দুটির গ.সা.গু.-এর মান খুঁজি ও ওই গ.সা.গু.-এর সাহায্যে ল.সা.গু.-এর মান খোঁজার চেষ্টা করি।

\(\therefore\) 145, 232-এর গ.সা.গু. = 29
আমরা জানি, সংখ্যা দুটির গ.সা.গু. \(\times\) ল.সা.গু = সংখ্যা দুটির গুণফল
বা, \(29\times\) ল.সা.গু. \(= 145\times 232\)
বা, ল.সা.গু \(=\frac{145 \times 232}{29}=1160\)
\(\therefore\) নির্ণেয় ল.সা.গু = 1160
Koshi Dakhi 12 Class 6 Math Solution || কষে দেখি 12 ক্লাস 6 || তিনটি সংখ্যার গ.সা.গু ও ল.সা.গু
15. 144 ও 384 সংখ্যা দুটির ল.সা.গু.-এর মান খুঁজি ও ওই ল.সা.গু.-এর সাহায্যে গ.সা.গু.-এর মান খোঁজার চেষ্টা করি।

\(\therefore\) 144, 384-এর লসাগু \( =2 \times 2 \times 2 \times 2 \times 3 \times 3 \times 8=1152 \)
আমরা জানি, সংখ্যা দুটির গাসাগু \(\times\) লসাগু = সংখ্যা দুটির গুণফল
বা, গসাগু \( \times 1152=144 \times 384 \)
\(\therefore\) গসাগু \( =\frac{144 \times 384}{1152}=48 \)
\(\therefore\) নির্ণেয় গসাগু = 48
16. 5834 থেকে কোন ক্ষুদ্রতম সংখ্যা বিয়োগ করলে বিয়োগফল 20, 28, 32, ও 35 দিয়ে বিভাজ্য হবে হিসেব করি।
20, 28, 32, 35 দিয়ে বিভাজ্য ক্ষুদ্রতম সংখ্যাটি হবে 20, 28, 32 ও 35-এর লসাগু

\(\therefore\) লসাগু \( =2 \times 2 \times 5 \times 7 \times 8=1120 \)
\(\therefore\) যে সংখ্যাটি 20, 28, 32, 35 দ্বারা বিভাজ্য হবে সেটি 1120 দ্বারাও বিভাজ্য হবে।

\(\therefore\) 5834 থেকে ক্ষুদ্রতম সংখ্যা 234 বিয়োগ করলে বিয়োগফল 20, 28, 32, 35 দ্বারা বিভাজ্য হবে।

\(\therefore\) লসাগু \( =2 \times 2 \times 5 \times 7 \times 8=1120 \)
\(\therefore\) যে সংখ্যাটি 20, 28, 32, 35 দ্বারা বিভাজ্য হবে সেটি 1120 দ্বারাও বিভাজ্য হবে।

\(\therefore\) 5834 থেকে ক্ষুদ্রতম সংখ্যা 234 বিয়োগ করলে বিয়োগফল 20, 28, 32, 35 দ্বারা বিভাজ্য হবে।
17. কোন্ বৃহত্তম সংখ্যা দিয়ে 2300 ও 3500-কে ভাগ করলে যথাক্রমে 32 ও 56 ভাগশেষ থাকবে হিসেব করি।
\( 2300-32=2268\)
\(3500-56=3444 \)
যেহেতু, ওই বৃহত্তম সংখ্যা দিয়ে 2300 ও 3500-কে ভাগ করলে যথাক্রমে 32 ও 56 ভাগশেষ হয়
\(\therefore\) 2268 ও 3444-কে বৃহত্তম সংখ্যাটি দিয়ে ভাগ করলে ভাগশেষ শূন্য হবে।
অতএব, 2268, 3444 সংখ্যা দুটির গসাগুই হবে নির্ণেয় বৃহত্তম সংখ্যা যার দ্বারা।

\(\therefore\) 2268, 3444-এর গসাগু = 84
\(\therefore\) নির্ণেয় বৃহত্তম সংখ্যা হল 84 যা দ্বারা 2300-কে ভাগ করলে 32 এবং 3500-কে ভাগ করলে 56 ভাগশেষ থাকবে।
\(3500-56=3444 \)
যেহেতু, ওই বৃহত্তম সংখ্যা দিয়ে 2300 ও 3500-কে ভাগ করলে যথাক্রমে 32 ও 56 ভাগশেষ হয়
\(\therefore\) 2268 ও 3444-কে বৃহত্তম সংখ্যাটি দিয়ে ভাগ করলে ভাগশেষ শূন্য হবে।
অতএব, 2268, 3444 সংখ্যা দুটির গসাগুই হবে নির্ণেয় বৃহত্তম সংখ্যা যার দ্বারা।

\(\therefore\) 2268, 3444-এর গসাগু = 84
\(\therefore\) নির্ণেয় বৃহত্তম সংখ্যা হল 84 যা দ্বারা 2300-কে ভাগ করলে 32 এবং 3500-কে ভাগ করলে 56 ভাগশেষ থাকবে।
18. হিসেব করে দেখি কোন বৃহত্তম সংখ্যা দিয়ে 650, 775 ও 1250-কে ভাগ করলে প্রতিক্ষেত্রে একই ভাগশেষ থাকবে।
\(775-650 = 125\)
\(1250-650= 600\)
\(\therefore\) 600 এবং 125-এর গসাগুই হল নির্ণেয় বৃহত্তম সংখ্যা
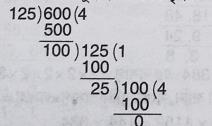
\(\therefore\) বৃহত্তম সংখ্যা 25 দ্বারা 650, 775, 1250-কে ভাগ করলে প্রতিক্ষেত্রে একই ভাগশেষ থাকবে।
\(1250-650= 600\)
\(\therefore\) 600 এবং 125-এর গসাগুই হল নির্ণেয় বৃহত্তম সংখ্যা
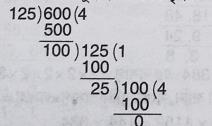
\(\therefore\) বৃহত্তম সংখ্যা 25 দ্বারা 650, 775, 1250-কে ভাগ করলে প্রতিক্ষেত্রে একই ভাগশেষ থাকবে।
19. দুটি সংখ্যার যোগফল 384 এবং সংখ্যা দুটির গ.সা.গু. 48; সংখ্যা দুটি কী কী হতে পারে হিসাব করি।
সংখ্যা দুটির গসাগু \( =48,384 \div 48=8 \)
এখন 8-কে দুটি সংখ্যার যোগফলের আকারে নিম্নলিখিতভাবে প্রকাশ করা যায়।
\( 8=1+7\)
\(=2+6\)
\(=3+5\)
\(=4+4 \)
এখন, (1, 7), (2, 6), (3, 5) ও (4, 4) -এই সংখ্যা জোড়গুলির মধ্যে (1, 7) ও (3, 5) পরস্পর মৌলিক।
এখানে পরস্পর মৌলিক জোড়গুলি নিলে গসাগু = 48 হবে।
\(\therefore\) সংখ্যাজোড়টি হবে, \( 48 \times 1=48,48 \times 7=336 \) এবং
অপর সংখ্যাজোড়টি হবে, \( 48 \times 3=144,48 \times 5=240 \)
\(\therefore\) সংখ্যা দুটি (48, 336) অথবা (144, 240) হতে পারে।
এখন 8-কে দুটি সংখ্যার যোগফলের আকারে নিম্নলিখিতভাবে প্রকাশ করা যায়।
\( 8=1+7\)
\(=2+6\)
\(=3+5\)
\(=4+4 \)
এখন, (1, 7), (2, 6), (3, 5) ও (4, 4) -এই সংখ্যা জোড়গুলির মধ্যে (1, 7) ও (3, 5) পরস্পর মৌলিক।
এখানে পরস্পর মৌলিক জোড়গুলি নিলে গসাগু = 48 হবে।
\(\therefore\) সংখ্যাজোড়টি হবে, \( 48 \times 1=48,48 \times 7=336 \) এবং
অপর সংখ্যাজোড়টি হবে, \( 48 \times 3=144,48 \times 5=240 \)
\(\therefore\) সংখ্যা দুটি (48, 336) অথবা (144, 240) হতে পারে।
Koshi Dakhi 12 Class 6 Math Solution || কষে দেখি 12 ক্লাস 6 || তিনটি সংখ্যার গ.সা.গু ও ল.সা.গু
20. দুটি সংখ্যার গ.সা.গু. ও ল.সা.গু. যথাক্রমে 12 ও 720; হিসাব করে দেখি এরকম কত জোড়া সংখ্যা হতে পারে এবং সম্ভাব্য সংখ্যাগুলি কী কী?
সংখ্যাদুটির গসাগু 12 ও লসাগু 720
সংখ্যাদ্বয়ের লসাগু-র মধ্যে গসাগু আছে \( (720 \div 12) \) বার = 60 বার
এখন 60-কে দুটি সংখ্যার গুণফল আকারে নিম্নলিখিতভাবে লেখা যায়।
\( 60 =1 \times 60\)
\(=2 \times 30\)
\(=3 \times 20\)
\(=4 \times 15\)
\(=5 \times 12\)
\(=6 \times 10 \)
এখানে, (1, 60); (2, 30); (3, 20); (4, 15); (5, 12); (6, 10)-এইসংখ্যা জোড়গুলিরমধ্যে (1, 60); (3, 20); (4, 15) ও (5, 12) সংখ্যা জোড়গুলি পরস্পর মৌলিক।
\(\therefore\) সংখ্যাগুলি হতে পারে,
\( 12 \times 1=12\)
\(12 \times 60=720 \)
\( 12 \times 3=36\)
\(12 \times 20=240 \)
\( 12 \times 4=48\)
\(12 \times 15=180 \)
\( 12 \times 5=60\)
\(12 \times 12=144 \)
\(\therefore\) সংখ্যাদ্বয় হতে পারে, (12, 720) বা (36, 240) বা (48, 180) বা (60, 144)।
সংখ্যাদ্বয়ের লসাগু-র মধ্যে গসাগু আছে \( (720 \div 12) \) বার = 60 বার
এখন 60-কে দুটি সংখ্যার গুণফল আকারে নিম্নলিখিতভাবে লেখা যায়।
\( 60 =1 \times 60\)
\(=2 \times 30\)
\(=3 \times 20\)
\(=4 \times 15\)
\(=5 \times 12\)
\(=6 \times 10 \)
এখানে, (1, 60); (2, 30); (3, 20); (4, 15); (5, 12); (6, 10)-এইসংখ্যা জোড়গুলিরমধ্যে (1, 60); (3, 20); (4, 15) ও (5, 12) সংখ্যা জোড়গুলি পরস্পর মৌলিক।
\(\therefore\) সংখ্যাগুলি হতে পারে,
\( 12 \times 1=12\)
\(12 \times 60=720 \)
\( 12 \times 3=36\)
\(12 \times 20=240 \)
\( 12 \times 4=48\)
\(12 \times 15=180 \)
\( 12 \times 5=60\)
\(12 \times 12=144 \)
\(\therefore\) সংখ্যাদ্বয় হতে পারে, (12, 720) বা (36, 240) বা (48, 180) বা (60, 144)।
21. কোন ক্ষুদ্রতম সংখ্যা থেকে 4000 বিয়োগ করলে বিয়োগফল 7, 11, ও 13 দিয়ে বিভাজ্য হবে হিসাব করি ।
7, 11, 13 দ্বারা বিভাজ্য ক্ষুদ্রতম সংখ্যাটি হবে 7, 11, 13-এর লসাগু।
\(\therefore\) লসাগু \( =7 \times 11 \times 13=1001 \)
\(\therefore\) নির্ণেয় সংখ্যাটি \(= 1001 + 4000 = 5001\);
\(\therefore\) ক্ষুদ্রতম সংখ্যা 5001 থেকে 4000 বিয়োগ করলে বিয়োগফল 7, 11, 13 দ্বারা বিভাজ্য হবে।
\(\therefore\) লসাগু \( =7 \times 11 \times 13=1001 \)
\(\therefore\) নির্ণেয় সংখ্যাটি \(= 1001 + 4000 = 5001\);
\(\therefore\) ক্ষুদ্রতম সংখ্যা 5001 থেকে 4000 বিয়োগ করলে বিয়োগফল 7, 11, 13 দ্বারা বিভাজ্য হবে।
22. 50 ও 100-এর মধ্যবর্তী দু-জোড়া সংখ্যা খুঁজি যাদের গ.সা.গু. 16
সংখ্যাগুলির গসাগু 16 হলে নির্ণেয় সংখ্যাজোড়গুলি অবশ্যই 16-এর গুণিতক হবে।
এখন, \( 16 \times 4=64\)
\(16 \times 5=80\)
\(16 \times 6=96 \)
\(\therefore\) 50 ও 100-এর মধ্যে দু-জোড়া সংখ্যা হল (64, 80), (80, 96) যাদের গসাগু = 16
এখন, \( 16 \times 4=64\)
\(16 \times 5=80\)
\(16 \times 6=96 \)
\(\therefore\) 50 ও 100-এর মধ্যে দু-জোড়া সংখ্যা হল (64, 80), (80, 96) যাদের গসাগু = 16
23. 28, 33, 42 ও 77 দ্বারা বিভাজ্য যে সংখ্যাটি 98765-এর নিকটতম তা হিসেব করে খুঁজে বার করি।
28, 33, 42, 77 দ্বারা বিভাজ্য ক্ষুদ্রতম সংখ্যাটি হল 28, 33, 42 ও 77-এর লসাগু ।

\(\therefore\) নির্ণেয় লসাগু \( =2 \times 2 \times 3 \times 7 \times 11=924 \)
\(\therefore\) যে সংখ্যাটি 28, 33, 42 ও 77 দ্বারা বিভাজ্য হবে সেটি 924 দ্বারাও বিভাজ্য হবে।

\(\therefore\) 98765-এর পূর্ববর্তী 924 দ্বারা বিভাজ্য নিকটতম পূর্ণসংখ্যা
\(= (98765-821) = 97944\)
\(\therefore\) 98765-এর পরবর্তী 924 দ্বারা বিভাজ্য নিকটতম পূর্ণসংখ্যা হল
\( =98765+(924-821)=98765+103=98868 \)
\( \because 103<821 \)
\(\therefore\) নির্ণেয় নিকটতম সংখ্যা 98868

\(\therefore\) নির্ণেয় লসাগু \( =2 \times 2 \times 3 \times 7 \times 11=924 \)
\(\therefore\) যে সংখ্যাটি 28, 33, 42 ও 77 দ্বারা বিভাজ্য হবে সেটি 924 দ্বারাও বিভাজ্য হবে।

\(\therefore\) 98765-এর পূর্ববর্তী 924 দ্বারা বিভাজ্য নিকটতম পূর্ণসংখ্যা
\(= (98765-821) = 97944\)
\(\therefore\) 98765-এর পরবর্তী 924 দ্বারা বিভাজ্য নিকটতম পূর্ণসংখ্যা হল
\( =98765+(924-821)=98765+103=98868 \)
\( \because 103<821 \)
\(\therefore\) নির্ণেয় নিকটতম সংখ্যা 98868
24. হিসেব করে 13 দিয়ে বিভাজ্য এমন ক্ষুদ্রতম সংখ্যা খুঁজি যা 8, 12, 16 ও 20 দিয়ে ভাগ করলে প্রতিক্ষেত্রে 1 ভাগশেষ থাকে।
8, 12, 16, 20 দ্বারা বিভাজ্য ক্ষুদ্রতম সংখ্যাটি হল 8, 12, 16, 20-এর লসাগু।

\(\therefore\) নির্ণেয় লসাগু \( =2 \times 2 \times 2 \times 3 \times 2 \times 5=240 \)
\(\therefore\) নির্ণেয় সংখ্যাটি 240-এর গুণিতক + 1 হবে যা 13 দ্বারা বিভাজ্য। \(240 \times 1 + 1 = 241\) – 13 দ্বারা বিভাজ্য নয়
\(240 \times 2 + 1 = 481\) – 13 দ্বারা বিভাজ্য
\(\therefore\) নির্ণেয় ক্ষুদ্রতম সংখ্যাটি হল 481, যা 13 দিয়ে বিভাজ্য।

\(\therefore\) নির্ণেয় লসাগু \( =2 \times 2 \times 2 \times 3 \times 2 \times 5=240 \)
\(\therefore\) নির্ণেয় সংখ্যাটি 240-এর গুণিতক + 1 হবে যা 13 দ্বারা বিভাজ্য। \(240 \times 1 + 1 = 241\) – 13 দ্বারা বিভাজ্য নয়
\(240 \times 2 + 1 = 481\) – 13 দ্বারা বিভাজ্য
\(\therefore\) নির্ণেয় ক্ষুদ্রতম সংখ্যাটি হল 481, যা 13 দিয়ে বিভাজ্য।
Koshi Dakhi 12 Class 6 Math Solution || কষে দেখি 12 ক্লাস 6 || তিনটি সংখ্যার গ.সা.গু ও ল.সা.গু
এই Page টি বা এই Website টির কোন প্রকার বিষয়বস্তু কপি করা বা সম্পাদনা করা নিষিদ্ধ। ভারতীয় Copywright আইন 1957 এর ধারা 63 অনুযায়ী, এই ফাইলটির সমস্ত অধিকার 'ছাত্র মিত্র Mathematics' অ্যাপ দ্বারা সংরক্ষিত। ছাত্র মিত্রের অনুমতি ছাড়া, এই Page টি বা এই Website টির কোন প্রকার বিষয়বস্তু কপি করা বা সম্পাদনা করা আইনত দন্ডনীয় অপরাধ। কেউ ছাত্র মিত্রের অনুমতি ছাড়া, এই Page টি বা এই Website টির কোন প্রকার বিষয়বস্তু কপি বা সম্পাদনা করলে ছাত্র মিত্র কতৃপক্ষ তার বিরুদ্ধে সকল প্রকার কঠোর আইনি পদক্ষেপ করবে।
West Bengal Board of Secondary Education Official Site
Class 8 : গণিত প্রভা (অষ্টম শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali.
Class 7 : গণিত প্রভা (সপ্তম শ্রেণি) বইয়ের সমস্ত সমাধান
www.wbresults.nic.in Official
Class 10 : মাধ্যমিক গণিত প্রকাশ (দশম শ্রেণি) বইয়ের সমস্ত সমাধান Class 10 Maths Solution WBBSE Bengali
Class 6 : গণিত প্রভা (ষষ্ঠ শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali
Class 9 : গণিত প্রকাশ (নবম শ্রেণি) বইয়ের সমাধান Maths Solution WBBSE Bengali
আজই Install করুন Chatra Mitra
Class 8 : গণিত প্রভা (অষ্টম শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali.
Class 7 : গণিত প্রভা (সপ্তম শ্রেণি) বইয়ের সমস্ত সমাধান
www.wbresults.nic.in Official
Class 10 : মাধ্যমিক গণিত প্রকাশ (দশম শ্রেণি) বইয়ের সমস্ত সমাধান Class 10 Maths Solution WBBSE Bengali
Class 6 : গণিত প্রভা (ষষ্ঠ শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali
Class 9 : গণিত প্রকাশ (নবম শ্রেণি) বইয়ের সমাধান Maths Solution WBBSE Bengali
আজই Install করুন Chatra Mitra



