(a)\(\triangle \mathrm{ABC}\)-এ PQ || BC,
\(\therefore\) থ্যালেসের উপপাদ্য অনুসারে,
\(\frac{\mathrm{AP}}{\mathrm{BP}}=\frac{\mathrm{AQ}}{\mathrm{CQ}}\)\(\ldots\ldots\)(1)।
বা, \(\frac{9}{\mathrm{AQ}}=\frac{\mathrm{AQ}}{4}\) \([\because \mathrm{AP}=9\) একক, \(\mathrm{QC}=4\) একক \(]\)
বা,\(\mathrm{AQ}^{2}=36\)
বা,\(A Q=\sqrt{36}\)
বা, \(\mathrm{AQ}=6\)
\(\therefore\) (1) থেকে পাই, \(\frac{9}{\mathrm{~PB}}=\frac{6}{4}\)
বা, \(P B=\frac{36}{6}\)
বা, \(P B=6\)
\(\therefore\) PB-এর দৈর্ঘ্য = 6 একক
(b) (a)-এর (1) থেকে পাই, \(\frac{\mathrm{AP}}{\mathrm{BP}}=\frac{\mathrm{AQ}}{\mathrm{CQ}}\)
বা, \(\frac{\mathrm{AP}}{2 \mathrm{AP}}=\frac{\mathrm{AQ}}{\mathrm{AQ}+3}\) [প্রশ্নানুসারে]
বা, \(\frac{1}{2}=\frac{A Q}{A Q+3}\)
বা, \(2 \mathrm{AQ}=\mathrm{AQ}+3\)
\(\therefore Q C=A Q+3=(3+3)\) একক = 6 একক
\(\therefore \mathrm{AC}=\mathrm{AQ}+\mathrm{QC}=(3+6)\) একক = 9 একক
\(\therefore\) AC -এর দৈর্ঘ্য = 9 একক
(c) -এর (1) নং থেকে পাই, \(\frac{\mathrm{AP}}{\mathrm{BP}}=\frac{\mathrm{AQ}}{\mathrm{CQ}}\)
বা, \(\frac{\mathrm{AP}+\mathrm{BP}}{\mathrm{BP}}=\frac{\mathrm{AQ}+\mathrm{CQ}}{\mathrm{CQ}}\)
বা,\(\frac{\mathrm{AB}}{\mathrm{PB}}=\frac{2+\mathrm{CQ}}{\mathrm{CQ}}\)
বা, \(\frac{12}{\mathrm{~PB}}=\frac{2+\mathrm{CQ}}{\mathrm{CQ}}\) \(\ldots\ldots\) (2)
আবার, \(\frac{\mathrm{AP}}{\mathrm{BP}}=\frac{\mathrm{AQ}}{\mathrm{CQ}}\)
বা, \(\frac{\mathrm{CQ}}{\mathrm{PB}}=\frac{2}{\mathrm{CQ}}\)
বা, \(2 \mathrm{~PB}=\mathrm{CQ}^{2}\)
বা, \(\mathrm{PB}=\frac{\mathrm{CQ}^{2}}{2}\)
\(\therefore\) (2) থেকে পাই ,
বা, \(\frac{12}{\frac{C Q^{2}}{2}}=\frac{2+C Q}{C Q}\)
বা, \(\frac{24}{\mathrm{CQ}^{2}}=\frac{2+\mathrm{CQ}}{\mathrm{CQ}}\)
বা, \(\frac{24}{\mathrm{CQ}}=2+\mathrm{CQ} [\because \mathrm{CQ} \neq 0]\) \([\because \mathrm{CQ} \neq 0]\)
বা, \(2 \mathrm{CQ}+\mathrm{CQ}^{2}=24\)
বা,\(\mathrm{CQ}^{2}+2 \mathrm{CQ}-24=0\)
বা, \(\operatorname{CQ}^{2}+(6-4) C Q-24=0\)
বা, \(\mathrm{CQ}(\mathrm{CQ}+6)-4(\mathrm{CQ}+6)=0\)
বা, \(C Q^{2}+6 C Q-4 C Q-24=0\)
বা, \((\mathrm{CQ}+6)(\mathrm{CQ}-4)=0\)
\(\therefore\) হয় \(\mathrm{CQ}+6=0\)
বা, \(\mathrm{CQ}=-6\) (গ্রাহ্য)
নতুবা, \(\mathrm{CQ}-4=0\)
বা, \(\mathrm{CQ}=4\)(গ্রাহ্য নয়)
কিন্তু CQ-এর মান ঋণাত্মক হতে পারে না।
\(\therefore\) CQ = 4 একক
\(\therefore\) CQ-এর দৈর্ঘ্য = 4 একক।

(a) \(\triangle \mathrm{PQR}\) -এ XY ও QR পরস্পর সমান্তরাল হবে যদি \(\frac{\mathrm{PX}}{\mathrm{QX}}=\frac{\mathrm{PY}}{\mathrm{RY}}\)
এখন,\(\frac{P X}{Q X}\)= \(\frac{\text{2 একক }}{\text{3.5 একক}}\) = \(\frac{2}{\frac{35}{10}}=2 \times \frac{10}{35}=\frac{4}{7}\)
আবার, \(\frac{P Y}{R Y}\) = \(\frac{\text{4.25 একক }}{\text{ 7 একক}}\) = \(\frac{425}{100} \times \frac{1}{7}=\frac{17}{28}\)
\(\therefore \frac{\mathrm{PX}}{\mathrm{QX}} \neq \frac{\mathrm{PY}}{\mathrm{RY}}\) \(\therefore X Y \not\| Q R\)

(b) \(\triangle \mathrm{PQR}\) -এ XY ও QR পরস্পর সমান্তরাল হবে যদি \(\frac{P X}{Q X}=\frac{P Y}{R Y}\) হয়। \(\ldots\ldots\)(1)
বা, \(\frac{\mathrm{PX}+\mathrm{QX}}{\mathrm{QX}}=\frac{\mathrm{PY}+\mathrm{RY}}{\mathrm{RY}}\)
\(\frac{\mathrm{PQ}}{\mathrm{QX}}=\frac{\mathrm{PY}+\mathrm{RY}}{\mathrm{RY}}\)
বা, \(\frac{8}{6}=\frac{4+12}{12}\) [\(\because\) PQ = 8 একক, \(P Y=4\) একক, \(\mathrm{YR}=12\)একক এবং \(Q X=(P Y+2)\) \(=(4+2)\) একক = 6 একক]
বা, \(\frac{4}{3}=\frac{16}{12}\)
বা, \(\frac{4}{3}=\frac{4}{3}\)
অর্থাৎ,\(\frac{\mathrm{PX}}{\mathrm{QX}}=\frac{\mathrm{PY}}{\mathrm{RY}}, \therefore \mathrm{XY} \| \mathrm{QR}\)
\(\therefore\) প্রদত্ত শর্তাধীনে XY ও QR পরস্পর সমান্তরাল হবে।

ধরি, \(\triangle \mathrm{ABC}\)-এর AB-এর মধ্যবিন্দু E এবং E বিন্দু থেকে BC-এর সমান্তরাল সরলরেখা EF, AC-কে F বিন্দুতে ছেদ করেছে।
প্রমাণ করতে হবে যে, F, AC-এর মধ্যবিন্দু, অর্থাৎ, AF = CF
প্রমাণ : \(\triangle \mathrm{ABC}\)-এ EF || BC (প্রদত্ত),
থ্যালেসের উপপাদ্য অনুসারে পাই,
\(\frac{\mathrm{AE}}{\mathrm{BE}}=\frac{\mathrm{AF}}{\mathrm{CF}}\)
বা, \(\frac{\mathrm{AE}}{\mathrm{AE}}=\frac{\mathrm{AF}}{\mathrm{CF}}\) [\(\because\) E, AB -এর মধ্যবিন্দু , \(\therefore\) AE=BE ]
বা, \(1=\frac{\mathrm{AF}}{\mathrm{CF}}\)
বা, \(\mathrm{AF}=\mathrm{CF}\)
\(\therefore\) F, AC-এর মধ্যবিন্দু, অর্থাৎ EF, AC-কে সমদ্বিখণ্ডিত করেছে। (প্রমাণিত)

ধরি, \(\triangle \mathrm{ABC}\)-এর AD মধ্যমার উপর P একটি বিন্দু। বর্ধিত BP ও বর্ধিত CP, AC ও AB-কে যথাক্রমে Q ও R বিন্দুতে ছেদ করেছে।
প্রমাণ করতে হবে যে, RQ || BC
অঙ্কন : PD-কে T পর্যন্ত এমনভাবে বর্ধিত করি যেন, PD = DT হয়। B, T এবং C, T যুক্ত করি। ।
প্রমাণ : BPCT চতুর্ভুজের BC ও PT দুটি কর্ণ। আবার, BD = CD [\(\because\) AD_ মধ্যমা] এবং PD = DT [অঙ্কনানুসারে) ।
অর্থাৎ, BPCT চতুর্ভুজের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে।
\(\therefore\) BPCT একটি সামান্তরিক।
\(\therefore \) BP \(\| \mathrm{TC}\) এবং \(\mathrm{TB} \| \mathrm{CP}\)
এখন, \(\triangle \mathrm{ABT}\)-এ RP || BT \(\lfloor\because\) TB \(\| \mathrm{CP}]\)
\(\therefore\) থ্যালেসের উপপাদ্য অনুসারে, \(\frac{\mathrm{AR}}{\mathrm{BR}}=\frac{\mathrm{AP}}{\mathrm{TP}}\) \(\ldots\ldots\)(1)
আবার, \(\triangle \mathrm{ACT}\)-এ QP || CT [ \(\because\) BP || TC]
\(\therefore\) থ্যালেসের উপপাদ্য অনুসারে, \(\frac{\mathrm{AQ}}{\mathrm{CQ}}=\frac{\mathrm{AP}}{\mathrm{TP}}\) \(\ldots\ldots\)(2)
তাহলে, (1) ও (2) থেকে পাই, \(\frac{\mathrm{AR}}{\mathrm{BR}}=\frac{\mathrm{AQ}}{\mathrm{CQ}}\)
\(\therefore\) \(\triangle \mathrm{ABC}\) -এ \(\frac{\mathrm{AR}}{\mathrm{BR}}=\frac{\mathrm{AQ}}{\mathrm{CQ}}\)
\(\therefore\) থ্যালেসের উপপাদ্যের বিপরীত উপপাদ্য অনুসারে, , \(\mathrm{RQ} \| \mid \mathrm{BC}\)
\(\therefore\) RQ || BC (প্রমাণিত)।

প্রদত্ত, \(\triangle \mathrm{ABC}\)-এর BE ও CF মধ্যমা পরস্পরকে G বিন্দুতে ছেদ করেছে। FE, AG-কে O বিন্দুতে ছেদ
করেছে। প্রমাণ করতে হবে যে, AO = 3OG
অঙ্কন : AG কে বর্ধিত করি। ধরি, বর্ধিত AG, BC-কে D বিন্দুতে ছেদ করেছে। তাহলে, G, \(\triangle \mathrm{ABC}\)-এর ভরকেন্দ্র এবং AD একটি মধ্যমা [\(\therefore\) ত্রিভুজের মধ্যমাগুলি সমবিন্দু]।
প্রমাণ : G, \(\triangle \mathrm{ABC}\)-এর ভরকেন্দ্র এবং AD মধ্যমা।
\(\therefore \mathrm{AG}: \mathrm{GD}=2: 1\) [কারণ, ত্রিভুজের ভরকেন্দ্র, মধ্যমাগুলিকে 2 : 1 অনুপাতে বিভক্ত করে।]
বা, \(\frac{\mathrm{AG}}{\mathrm{GD}}=\frac{2}{1}\)
বা, \(\frac{\mathrm{AO}+\mathrm{OG}}{\mathrm{OD}-\mathrm{OG}}=\frac{2}{1}\) [চিত্রানুসারে,]
বা,\(2 O D-2 O G=A O+O G\)
বা,\(2 O D-A O=O G+2 O G\)
বা,\(2 \mathrm{AO}-\mathrm{AO}=3 \mathrm{OG}\)
[\(\because \triangle \mathrm{ABD}-\)এ FO|| BD, (মধ্যবিন্দুদ্বয়ের সংযােজক রেখাংশ তৃতীয় বাহুর সমান্তরাল)
\(\therefore \frac{\mathrm{AF}}{\mathrm{BF}}=\frac{\mathrm{AO}}{\mathrm{OD}}\)
বা, \(\frac{\mathrm{AF}}{\mathrm{AF}}=\frac{\mathrm{AO}}{\mathrm{OD}}(\because \mathrm{AF}=\mathrm{BF})\)
বা, \(1=\frac{\mathrm{AO}}{\mathrm{OD}} \Rightarrow \mathrm{AO}=\mathrm{OD}\), i.e., \(\left.\mathrm{OD}=\mathrm{AO}\right]\)
বা, AO = 30G (প্রমাণিত)

ধরি, ABCD একটি ট্রাপিজিয়াম যার AD ও BC বাহুদ্বয় সমান্তরাল, অর্থাৎ AD || BC। AB ও DC এটির দুটি তির্যক বাহু, মধ্যবিন্দু দুটি যথাক্রমে E ও F।
প্রমাণ করতে হবে যে, EF || AD এবং EF || BC
অঙ্কন : BA ও CD-কে বর্ধিত করি। ধরি, বর্ধিত BA ও বর্ধিত CD পরস্পরকে P বিন্দুতে ছেদ করেছে।
প্রমাণ : \(\triangle \mathrm{PCB}\)-এ \(\mathrm{AD} \| \mathrm{BC}\) \(\therefore\) থ্যালেসের উপপাদ্য অনুসারে,
\(\frac{\mathrm{PA}}{\mathrm{AB}}=\frac{\mathrm{PD}}{\mathrm{DC}}\)
বা,\(\frac{\mathrm{PA}}{2 \mathrm{AE}}=\frac{\mathrm{PD}}{2 \mathrm{DF}}\) [ \(\because\) E ও F যথাক্রমে AB ও AC -এর মধ্যবিন্দু। ]
\(\frac{\mathrm{PA}}{\mathrm{AE}}=\frac{\mathrm{PD}}{\mathrm{DF}}\)
\(\therefore \triangle \mathrm{PEF}\) এ \(\frac{\mathrm{PA}}{\mathrm{AE}}=\frac{\mathrm{PD}}{\mathrm{DF}}\)
\(\therefore\) থ্যালেসের উপপাদ্যের বিপরীত উপপাদ্য অনুসারে, EF || AD
আবার, \(\because \mathrm{AD}\|\mathrm{BC}, \therefore \mathrm{AD}\| \mathrm{EF} \| \mathrm{BC} .\) (প্রমাণিত)

ধরি, \(\triangle \mathrm{ABC}\)-এর BC বাহুর উপর D যে-কোনাে একটি বিন্দু। \(\triangle \mathrm{ABD}\)-এর BE ও DF মধ্যমা দুটি পরস্পরকে P বিন্দুতে এবং \(\triangle \mathrm{ACD}\)-এর CE ও DS মধ্যমা দুটি পরস্পরকে Q বিন্দুতে ছেদ করেছে।
\(\therefore\) P ও Q যথাক্রমে \(\triangle ABD \) ও \(\triangle \mathrm{ADC}\) -এর ভরকেন্দ্র। P ও Q যুক্ত করি।
প্রমাণ করতে হবে যে, PQ || BC
প্রমাণ : P, \(\triangle \mathrm{ABD}\)-এর ভরকেন্দ্র। \(\therefore \frac{\mathrm{BP}}{\mathrm{PE}}=\frac{2}{1}\) [\(\therefore\) ভরকেন্দ্র মধ্যমাকে 2 : 1 অনুপাতে অন্তর্বিভক্ত করে] বা \(\mathrm{BP}=2 \mathrm{PE}\) \(\ldots\ldots\) (1)
অনুরূপভাবে, CQ = 2QE \(\ldots\ldots\) (2)
এখন, \(\triangle \mathrm{EBC}\) -এ \(\frac{\mathrm{EP}}{\mathrm{BP}}=\frac{\mathrm{EP}}{2 \mathrm{EP}}=\frac{1}{2}\) [(1) থেকে ] \(\ldots\ldots\)(3)
আবার, \(\triangle \mathrm{EBC}\)-এ \(\frac{\mathrm{EQ}}{\mathrm{CQ}}=\frac{\mathrm{EQ}}{2 \mathrm{EQ}}=\frac{1}{2}\) [(2) থেকে] \(\ldots\ldots\)(4)
(3) ও (4) থেকে আমরা পাই, \(\frac{\mathrm{EP}}{\mathrm{BP}}=\frac{\mathrm{EQ}}{\mathrm{CQ}}\)
অর্থাৎ, \(\Delta \mathrm{EBC}\) -এ PQ সরলরেখাটি BE ও CF-কে এমনভাবে বিভক্ত করেছে যে, \(\frac{\mathrm{EP}}{\mathrm{BP}}=\frac{\mathrm{EQ}}{\mathrm{CQ}}\)
\(\therefore\) থ্যালেসের উপপাদ্যের বিপরীত উপপাদ্য অনুসারে, PQ || BC
\(\therefore \mathrm{PQ} \| \mathrm{BC} .\) (প্রমাণিত) |

ধরি, \(\triangle \mathrm{PQR}\)ও \(\triangle \mathrm{SQR}\) একই ভূমি QR -এর উপর এবং QR-এর একই পার্শ্বে অবস্থিত দুটি ত্রিভুজ যাদের ক্ষেত্রফল সমান।
F ও G যথাক্রমে \(\triangle \mathrm{PQR}\)ও \(\triangle \mathrm{SQR}\)-এর ভরকেন্দ্র। F, G যুক্ত করা হল।
প্রমাণ করতে হবে যে, FG || QR
অঙ্কন : ধরি, T, QR-এর মধ্যবিন্দু।।
\(\therefore \mathrm{F}, \mathrm{PT}\) মধ্যমার উপর অবস্থিত হবে। \(P, T\) যুক্ত করি। একইভাবে, G, ST-এর উপর অবস্থিত হবে। S, T যুক্ত করি।
প্রমাণ : F, \(\triangle \mathrm{PQR}\)-এর ভরকেন্দ্র এবং PT একটি মধ্যম।
\(\therefore\) PF : FT = 2 : 1 [ \(\because\) ভরকেন্দ্র ত্রিভুজের মধ্যমাকে 2 : 1 আনুপাতে বিভক্ত করে।]
বা, \(\frac{\mathrm{PF}}{\mathrm{FT}}=\frac{2}{1}\)
বা, \(\mathrm{PF}=2 \mathrm{FT}\) \(\ldots\ldots\)(1)
একইভাবে, SG = 2GT \(\ldots\ldots\) (2)
এখন, \(\triangle P S T\)-এ FG সরলরেখাংশ PT-কে F বিন্দুতে এবং ST-কে G বিন্দুতে ছেদ করেছে, যেখানে,
\(\frac{P F}{F T}=\frac{2 F T}{F T}=2\) এবং\(\frac{\mathrm{SG}}{\mathrm{GT}}=\frac{2 \mathrm{GT}}{\mathrm{GT}}=2\)
অর্থাৎ, \(\frac{\mathrm{PF}}{\mathrm{FT}}=\frac{\mathrm{SG}}{\mathrm{GT}} \quad \therefore \mathrm{FG} \| \mathrm{PS}\)\(\ldots\ldots\)(3)
আবার, একই ভূমি QR-এর উপর এবং QR-এর একই পার্শ্বে \(\triangle \mathrm{PQR}\)ও \(\triangle \mathrm{SQR}\) অবস্থিত যাদের ক্ষেত্রফল সমান।
\(\therefore\) এরা একই সমান্তরাল যুগলের মধ্যে অবস্থিত।
\(\therefore\) PS || QR \(\ldots\ldots\) (4)
তাহলে, (3) ও (4) থেকে পাই, FG || PS || QR
\(\therefore\) FG || QR. (প্রমাণিত)

প্রদত্ত : ধরি, ABCD একটি সমদ্বিবাহু ট্রাপিজিয়াম, যার AD = BC এবং AB || DC এবং \(\angle ADC \) ও \(\angle B C D, D C\), বাহুর সংলগ্ন দুটি কোণ।
প্রমাণ করতে হবে যে, \(\angle ADC \) = \(\angle \mathrm{BCD}\)
অকন : DA ও CB-কে বর্ধিত করি। ধরি, বর্ধিত DA ও বর্ধিত CB পরস্পরকে CB পরস্পরকে O বিন্দুতে ছেদ করেছে।
প্রমাণ : \(\triangle \mathrm{ODC}\)-এ AB || DC (প্রদত্ত), \(\therefore\) থ্যালেসের উপপাদ্য অনুসারে, \(\frac{\mathrm{OA}}{\mathrm{AD}}=\frac{\mathrm{OB}}{\mathrm{BC}}\)
বা, \(\frac{\mathrm{OA}}{\mathrm{BC}}=\frac{\mathrm{OB}}{\mathrm{BC}}\)\([\because \mathrm{AD}=\mathrm{BC}]\)
বা, \(\mathrm{OA}=\mathrm{OB}\)
এখন, \(\mathrm{OD}=\mathrm{OA}+\mathrm{AD}=\mathrm{OB}+\mathrm{BC}=\mathrm{OC}\) [\(\because \mathrm{OA}=\mathrm{OB}\) এবং \(A D=B C\)]
\(\therefore \mathrm{OD}=\mathrm{OC} \therefore \angle \mathrm{ODC}=\angle \mathrm{OCD}\)
বা, \(\angle \mathrm{ADC}=\angle \mathrm{BCD}\)
\(\therefore \angle \mathrm{ADC}=\angle \mathrm{BCD}\)(প্রমাণিত)

ধরি , \(\triangle \mathrm{ABC}\) ও \(\triangle \mathrm{DBC}\) একই ভূমি BC-এর উপর এবং BC-এর একই পার্শ্বে অবস্থিত। BC বাহুর উপর E যে-কোনাে একটি বিন্দু।
E বিন্দু দিয়ে AB এবং BD-এর সমান্তরাল সরলরেখা AC এবং DC বাহুকে যথাক্রমে F ও G বিন্দুতে ছেদ করে।
প্রমাণ করতে হবে যে, AD || FG
প্রমাণ : \(\triangle \mathrm{ABC}\)-এ FE || AB, \(\therefore\) থ্যালেসের উপপাদ্য অনুসারে,
\(\frac{\mathrm{CF}}{\mathrm{FA}}=\frac{\mathrm{CE}}{\mathrm{EB}}\)\(\ldots\ldots\)(1)
একইভাবে, \(\triangle \mathrm{BCD}\)-এ GE || DB, \(\therefore\) থ্যালেসের উপপাদ্য অনুসারে,
\(\frac{\mathrm{CG}}{\mathrm{GD}}=\frac{\mathrm{CE}}{\mathrm{EB}}\)\(\ldots\ldots\)(2)
(1) ও (2) থেকে পাই \(\frac{\mathrm{CF}}{\mathrm{FA}}=\frac{\mathrm{CG}}{\mathrm{GD}}\)
\(\therefore \triangle \mathrm{ACD}\)-এ FG, AC ও DC-কে এমনভাবে বিভক্ত করেছে যে, \(\frac{\mathrm{CF}}{\mathrm{FA}}=\frac{\mathrm{CG}}{\mathrm{GD}}\) \(\therefore\) থ্যালেসের উপপাদ্যের বিপরীত উপপাদ্য অনুসারে, \(\mathrm{FG}\|\mathrm{AD} \therefore \mathrm{AD}\| \mathrm{FG}\) (প্রমাণিত)

ABC ত্রিভুজের BC \(\|\) XY
\(\therefore {\rm{ }}\frac{{{\rm{AX}}}}{{{\rm{XB}}}}{\rm{ = }}\frac{{{\rm{AY}}}}{{{\rm{YC}}}}\)
বা, \(\frac{{{\rm{2}}{\rm{.4}}}}{{{\rm{XB}}}} = \frac{{3.2}}{{4.8}}\)\([A X=2.4, A Y=3.2, Y C=4.8]\)
বা, \({\rm{XB}} = \frac{{4.8 \times 2:4}}{{3.2}} = 3.6\)
\(\therefore {\rm{AB = AX + XB = 2}}{\rm{.4 + 3}}{\rm{.6 = 6}}\)
(b) 6 সেমি.
\(\therefore\) AB -এর দৈর্ঘ্য 6 সেমি

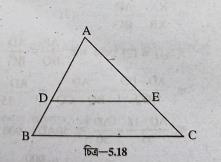
\(\triangle \mathrm{ABC}\)-এর DE || BC,
থ্যালেসের উপপাদ্য অনুসারে, \(\frac{\mathrm{AD}}{\mathrm{BD}}=\frac{\mathrm{AE}}{\mathrm{CE}}\)
বা,\(\frac{\mathrm{BD}}{\mathrm{AD}}=\frac{\mathrm{CE}}{\mathrm{AE}}\)
বা, \(\frac{\mathrm{BD}+\mathrm{AD}}{\mathrm{AD}}=\frac{\mathrm{CE}+\mathrm{AE}}{\mathrm{AE}}\)
বা, \(\frac{4}{3}=\frac{\mathrm{AC}}{3.3}\) \(\left[\because \mathrm{AD}: \mathrm{DB}=3: 1, \therefore \frac{\mathrm{BD}}{\mathrm{AD}}=\frac{1}{3}\right.\)
বা, \(\left.\frac{\mathrm{AD}+\mathrm{BD}}{\mathrm{AD}}=\frac{3+1}{3}=\frac{4}{3}\right]\)
বা, \(3 \mathrm{AC}=4 \times 3.3\)
বা, \(\mathrm{AC}=\frac{4 \times 3.3}{3}\)
\(=\frac{4 \times 33}{3 \times 10}\)
\(=\frac{4 \times 11}{10}\)
\(=\frac{44}{10}\)
বা, \(\mathrm{AC}=4.4\)
\(\therefore\) AC = 4.4 সেমি,
\(\therefore\) (e) উত্তরটি সঠিক।

\(\triangle \mathrm{ABC}\)-এ DE || BC
\(\therefore\) থ্যালেসের উপপাদ্য অনুসারে, \(\frac{\mathrm{AD}}{\mathrm{BD}}=\frac{\mathrm{AE}}{\mathrm{CE}}\)
বা, \(\frac{x+3}{3 x+19}=\frac{x}{3 x+4}\)
বা, \((3 x+4)(x+3)=x(3 x+19)\)
বা, \(3 x^{2}+4 x+9 x+12=3 x^{2}+19 x\)
বা, \(13 x-19 x+12=0\)
বা, \(3 x^{2}+13 x+12=3 x^{2}+19 x = 0\)
বা, \(-6 x+12=0\)
বা, \(6 x=12\)
বা, \(x=\frac{12}{6}=2\)
\(\therefore x\)-এর মান 2,
\(\therefore\) (d) উত্তরটি সঠিক।

ABCD ট্রাপিজিয়ামের AB || DC
অঙ্কন: ট্রাপিজিয়ামের DA ও CB বাহুকে বর্ধিত করি। ধরি, বর্ধিত DA ও বর্ধিত CB পরস্পরকে X বিন্দুতে ছেদ করেছে। এখন, \(\triangle \mathrm{XPQ}\)-এ \(\mathrm{AB} \| \mathrm{PQ}\) \([\because P Q \| D C \text{এবং} \mathrm{AB} \| \mathrm{DC}\) ]
\(\therefore\) থ্যালেসের উপপাদ্য অনুসারে, \(\frac{X A}{A P}=\frac{X B}{B Q}\)
বা, \(\frac{\mathrm{XA}}{\mathrm{XB}}=\frac{\mathrm{AP}}{\mathrm{BQ}}\) \(\ldots\ldots\) (1)
আবার, \(\triangle \mathrm{XCD}\)-এ AB || DC
\(\therefore\) থ্যালেসের উপপাদ্য অনুসারে, \(\frac{\mathrm{XA}}{\mathrm{AD}}=\frac{\mathrm{XB}}{\mathrm{BC}}\)
বা, \(\frac{\mathrm{XA}}{\mathrm{XB}}=\frac{\mathrm{AD}}{\mathrm{BC}}\) \(\ldots\ldots\)(2)
(1) ও (2) থেকে পাই,
\(\frac{\mathrm{AP}}{\mathrm{BQ}}=\frac{\mathrm{AD}}{\mathrm{BC}}\)
বা, \(\frac{\mathrm{AD}-\mathrm{PD}}{\mathrm{BQ}}=\frac{\mathrm{AD}}{\mathrm{BQ}+\mathrm{CQ}}\)
বা, \(\frac{\mathrm{AD}-18}{35}=\frac{\mathrm{AD}}{35+15}\) [\(\therefore\) PD = 18 সেমি, BQ = 35 সেমি, CQ = 15 সেমি।
বা, \(\frac{\mathrm{AD}-18}{35}=\frac{\mathrm{AD}}{50}\)
বা, \(50 \mathrm{AD}-900=35 \mathrm{AD}\)
বা, \(50 A D-35 A D=900\)
বা, \(15 \mathrm{AD}=900\)
বা, \(\mathrm{AD}=\frac{900}{15}=60\)
\(\therefore \mathrm{AD}=60\) সেমি
\(\therefore\) (a) উত্তরটি সঠিক।

আমরা জানি, \(\frac{\text{6 সেমি}}{\text{15 সেমি}}\) \(=\frac{1}{3}\) এবং \(\frac{\text{6 সেমি}}{\text{18 সেমি}}\) সেমি =\(\frac{1}{3}\)
\(\therefore\)\(\frac{\text{5 সেমি}}{\text{15 সেমি}}\)=\(\frac{\text{6 সেমি}}{\text{18 সেমি}}\)
বা, \(\frac{\mathrm{DP}}{\mathrm{DE}}=\frac{\mathrm{DQ}}{\mathrm{QF}}\)
অর্থাৎ \(\triangle \mathrm{DEF}\)-এ \(\frac{\mathrm{DP}}{\mathrm{DE}}=\frac{\mathrm{DQ}}{\mathrm{QF}} \Rightarrow \frac{\mathrm{DP}}{\mathrm{PE}} \neq \frac{\mathrm{DQ}}{\mathrm{QF}}\)
\(\therefore\) থ্যালেসের উপপাদ্যের বিপরীত উপপাদ্য অনুসারে,
\(PQ \not\| EF\)
\(\therefore\) (d) উত্তরটি সঠিক।

মিথ্যা। কারণ দুটি সদৃশ ত্রিভুজ সর্বদা সর্বসম নয়।

সত্য।

সমানুপাতে

সমান।

সমানুপাতে।

\(\triangle \mathrm{ABC}\) -এ \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
\(\therefore\) থ্যালেসের উপপাদ্যের বিপরীত উপপাদ্য অনুসারে, DE || BC
\(\therefore \angle \mathrm{ADE}\) = অনুরূপ\(\angle \mathrm{ABC}\)
বা, \(\angle \mathrm{ACB}=\angle \mathrm{ABC}\) [\(\therefore\) দেওয়া আছে, \(\angle \mathrm{ADE}=\angle \mathrm{ACB}\)]
\(\therefore \mathrm{AB}=\mathrm{AC}\)
\(\triangle ABC \) ত্রিভুজটি সমদ্বিবাহু।

\(\triangle A B C\)-এ DE || BC,
\(\therefore\) থ্যালেসের উপপাদ্য অনুসারে, \(\frac{\mathrm{AD}}{\mathrm{BD}}=\frac{\mathrm{AE}}{\mathrm{CE}} .\) \(\ldots\ldots\)(1)
আবার, দেওয়া আছে, \(\mathrm{AD}: \mathrm{BD}=3: 5\)
বা, \(\frac{\mathrm{AD}}{\mathrm{BD}}=\frac{3}{5}\)
\(\therefore \frac{\mathrm{AE}}{\mathrm{CE}}=\frac{3}{5}\)\(\ldots\ldots\) (2)
এখন, AE ও CE একই সরলরেখায় অবস্থিত এবং \(\triangle ADE \) ও \(\Delta \mathrm{CDE}\)-এর সাধারণ শীর্ষবিন্দু D, \(\therefore\) উভয় ত্রিভুজের উচ্চতা সমান হবে। ধরি, উক্ত সমান উচ্চতা = \(h\)
\(\therefore\) \(\frac{\text{\(\triangle \mathrm{ADE}\)-এর ক্ষেত্রফল}}{\text{\(\triangle \mathrm{CDE}\)-এর ক্ষেত্রফল}}\)=\(\frac{\frac{1}{2} \times \mathrm{AE} \times h}{\frac{1}{2} \times \mathrm{CE} \times h}=\frac{\mathrm{AE}}{\mathrm{CE}}=\frac{3}{5}\) [(2) থেকে পাই ]
\(\therefore\) নির্ণেয় অনুপাত = 3 : 5

\(\triangle \mathrm{ABC}\)-এ LM || AB
\(\therefore\) থ্যালেসের উপপাদ্য অনুসারে, \(\frac{\mathrm{CL}}{\mathrm{AL}}=\frac{\mathrm{CM}}{\mathrm{BM}}\)
বা, \(\frac{\mathrm{CL}+\mathrm{AL}}{\mathrm{AL}}=\frac{\mathrm{CM}+\mathrm{BM}}{\mathrm{BM}}\)
বা, \(\frac{\mathrm{AC}}{\mathrm{AL}}=\frac{\mathrm{BC}}{\mathrm{BM}}\)
বা, \(\frac{2 x}{x-3}=\frac{2 x+3}{x-2}\)
বা, \(2 x^{2}-6 x+3 x-9=2 x^{2}-4 x\)
বা, \(-3 x-9=-4 x\)
বা, \(-3 x+4 x=9\)
বা, \(x \quad \therefore x=9\) \(\therefore\) নির্ণেয় \(x\) -এর মান = 9।

\(\triangle \mathrm{APQ}\)-এ DE | | PQ,
\(\therefore\) থ্যালেসের উপপাদ্য অনুসারে, \(\frac{\mathrm{AD}}{\mathrm{DP}}=\frac{\mathrm{AE}}{\mathrm{EQ}}\)
বা, \(\frac{\text{3 সেমি}}{\text{\(x\) সেমি}}\)= \(\frac{\text{4 সেমি}}{\text{5 সেমি}}\) [\(\therefore\) AD = 3 সেমি, DP = \(x\) সেমি, AE = 4 সেমি এবং EQ = 5 সেমি]।
বা, \(\frac{3}{x}=\frac{4}{5}\)
বা, \(4 x=15\)
বা, \(\dot{x}=\frac{15}{4}\)
আবার, \(\triangle \mathrm{ABC}\)-এ PQ || BC,
\(\therefore\) থ্যালেসের উপপাদ্য অনুসারে, \(\frac{\mathrm{AP}}{\mathrm{PB}}=\frac{\mathrm{AQ}}{\mathrm{QC}}\)
বা, \(\frac{\mathrm{AD}+\mathrm{DP}}{\mathrm{PB}}=\frac{\mathrm{AE}+\mathrm{EQ}}{\mathrm{QC}}\) [চিত্রানুসারে]
বা, \(\frac{\text{3 সেমি+ \(x\) সেমি }}{\text{4 সেমি}}\) =\(\frac{\text{4 সেমি+ 5 সেমি }}{\text{\(y\) সেমি}}\)
বা, \(\frac{3+x}{4}=\frac{9}{y}\)
বা, \(\frac{3+\frac{15}{4}}{4}=\frac{9}{y}\left[\because x=\frac{15}{4}\right]\)
বা, \(\frac{\frac{12+15}{4}}{4}=\frac{9}{y}\)
বা, \(\frac{\frac{27}{4}}{4}=\frac{9}{y}\)
বা, \(\frac{3}{16}=\frac{1}{y}\)
বা, \(\frac{27}{16}=\frac{9}{y}\)
বা, \(3 y=16\)
বা, \(y=\frac{16}{3}\)
\(\therefore x=\frac{15}{4}\) এবং \(y=\frac{16}{3}\)

\(\triangle \mathrm{ABC}\)-এ DE || BC,
\(\therefore\) থ্যালেসের উপপাদ্য অনুসারে,
\(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
বা, \(\frac{\mathrm{AE}}{\mathrm{EC}}=\frac{2}{1}\left[\because \frac{\mathrm{AD}}{\mathrm{DB}}=\frac{2}{1}\right]\)
বা, \(\mathrm{AE}=2 \mathrm{EC}\) \(\ldots\ldots\) (1)
আবার, \(\triangle \mathrm{AXC}\)-এ BE || XC,
\(\therefore\) থ্যালেসের উপপাদ্য অনুসারে,
\(\frac{\mathrm{AB}}{\mathrm{BX}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
বা, \(\frac{\mathrm{AB}}{\mathrm{XB}}=\frac{2 \mathrm{EC}}{\mathrm{EC}}\) [(1) থেকে)]
বা, \(\frac{A B}{X B}=2\)
বা, \(\frac{\mathrm{AB}}{\mathrm{XB}}+1=2+1\)[উভয়দিকে 1 যোগ করে]
বা, \(\frac{A B+X B}{X B}=3\)
বা, \(\frac{\mathrm{AX}}{\mathrm{XB}}=\frac{3}{1} \)
বা, \(\frac{A X}{X B}=3\)
\(\therefore \frac{\mathrm{AX}}{\mathrm{XB}}\) এর মান \(= 3\)