WBBSE Class 8 Koshe dekhi 16.1 || ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই কষে দেখি 16.1 || WBBSE Class-8 (VIII) Koshe dekhi 16.1 Somadhan || Gonitprava Class 8 Chapter 16 Solution || গণিতপ্রভা অষ্টম শ্রেণি (ক্লাস-৮) সমাধান || West Bengal Board Class 8 Math Book Solution || অধ্যায় ১৬ পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদ
Share this page using :
WBBSE Class-8 (VIII) Koshe dekhi 16.1 WBBSE Class 8 Math Solution || ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই কষে দেখি 16.1 || WBBSE Class-8 (VIII) Koshe dekhi 16.1 Somadhan || West Bengal Board Class 8 Math Book Solution || অধ্যায় ১৬ পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদ
কষে দেখি - 16.1
1. নীচের প্রতিক্ষেত্রে \((x\)) -এর মান লিখি:
WBBSE Class-8 (VIII) Koshe dekhi 16.1 WBBSE Class 8 Math Solution || ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই কষে দেখি 16.1 || WBBSE Class-8 (VIII) Koshe dekhi 16.1 Somadhan || West Bengal Board Class 8 Math Book Solution || অধ্যায় ১৬ পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদ
(i)



\(DC\) রেখাকে বর্ধিত করা হল যা \(AB\) রেখাকে \(F\) বিন্দুতে ছেদ করে।
এবার \(\triangle \mathrm{DAF}\) এবং \(\triangle \mathrm{BFC}\) তৈরি হল।
\(\triangle \mathrm{DAF}\)-এর \(\angle DFA\) \( =180^{\circ}-\left(60^{\circ}+20^{\circ}\right)=100^{\circ} \)
অর্থাৎ, \( \angle C F A=100^{\circ} \)
\(\triangle \mathrm{CFB}\)-এর বহিস্থ কোণ \(\angle CFA \)
= অন্তঃস্থ বিপরীত \((\angle \mathrm{FBC}+\angle \mathrm{BCF})=40^{\circ}+\angle \mathrm{BCF}\)
\(\therefore \angle B C F=100^{\circ}-40^{\circ}=60^{\circ}\)
এখন, \(\angle B C D+\angle B C F=180^{\circ}\)
\(\therefore\) \( x+60^{\circ}=180^{\circ}\)
\(x=180^{\circ}-60^{\circ}\)
বা, \(x=120^{\circ}\)
(ii) 

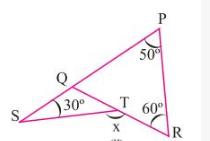
\( \triangle \mathrm{PQR} \)-এর
\(\angle P+\angle Q+\angle R=180^{\circ}\)
বা, \(50^{\circ}+\angle Q+60^{\circ}=180^{\circ}\)
বা, \(\angle Q+110^{\circ}=180^{\circ}\)
বা, \(\angle Q=180^{\circ}-110^{\circ}=70^{\circ}\)
এখন \(\triangle S Q T\) এর বহিস্থ কোণ \(\angle \mathrm{PQR}\)
= অন্তঃস্থ বিপরীত কোণ \((\angle \mathrm{QST}+\angle \mathrm{QTS})\)
বা, \(70^{\circ}=30^{\circ}+\angle \mathrm{QTS}\)
বা, \(70^{\circ}-30^{\circ}=\angle \mathrm{QTS}\)
বা, \(\angle \mathrm{QTS}=40^{\circ}\)
আবার, \(\angle \mathrm{QTS}+\angle \mathrm{STR}=180^{\circ}\)
বা, \(40^{\circ}+x=180^{\circ}\)
বা, \(x=180^{\circ}-40^{\circ}=140^{\circ}\)
(iii) 


\( \mathrm{PQ} \| \mathrm{TS} \) এবং \(QT\) ভেদক \(\angle \mathrm{QTS} \) = একান্তর \( \angle \mathrm{TQP}=55^{\circ} \)
আবার, \(\triangle \mathrm{RTS}\)-এর ক্ষেত্রে,
বা, \(\angle \mathrm{R}+\angle \mathrm{T}+\angle \mathrm{S}=180^{\circ}\)
বা, \(x+55^{\circ}+60^{\circ}=180^{\circ}\)
বা, \(x=180^{\circ}-115^{\circ}=65^{\circ}\)
2. পাশের চিত্রে \(\Delta\) EHGএর কোণগুলির পরিমাপ লিখি।



এখানে \( A B \| C D \) এবং \( EF \) ভেদক।
\(\therefore \angle \mathrm{CHE}=\) অনুরূপ \(\angle \mathrm{AFH}=110^{\circ}\)
\( \therefore \Delta \mathrm{EHG}\)-এ র \( \angle \mathrm{EHG}=180^{\circ}-\angle \mathrm{CHE} \)
\( =180^{\circ}-110^{\circ}=70^{\circ} \)
\(\angle \mathrm{HEG}=180^{\circ}-(\angle \mathrm{EHG}+\angle \mathrm{HGE})\)
\(=180^{\circ}-\left(70^{\circ}+60^{\circ}\right)=180^{\circ}-130^{\circ}=50^{\circ}\)
\(\therefore \Delta \mathrm{EHG}\)-এর কোণগুলি হল \( 60^{\circ}, 70^{\circ}, 50^{\circ} \)
3. পাশের চিত্রে \(\angle A+\angle B+\angle C+\angle D+\angle E+\angle F\) –এর পরিমাপ
লিখি।


চিত্রানুসারে, \(\angle E O F\) = বিপ্রতীপ \(\angle B O C\)
\(\angle A O B\) = বিপ্রতীপ \(\angle D O E\)
\(\angle C O D\) = বিপ্রতীপ \(\angle A O F\)
\(\angle E O F+\angle A O B+\angle C O D\)
\( =\angle B O C+\angle D O E+\angle A O F \)
\(=\frac{1}{2} \times 360^{\circ}=180^{\circ}\) ...(i) [(\(O\) বিন্দুতে মোট কোণ \(= 360^{\circ}\)]
আবার, একটি ত্রিভুজের \(3\) টি অন্তঃকোণের সমষ্টি \(= 180^{\circ}\)
\(\therefore\) \(3\) টি ত্রিভুজের মোট কোণ \( = 3 \times 180^{\circ} = 540^{\circ} \)
\( \therefore \angle A+\angle B+\angle C+\angle D+\angle E+\angle F+\angle E O F+\)
\(\quad \quad \quad \quad \quad \quad \angle A O B+\angle C O D=540^{\circ} \)
বা, \(\angle \mathrm{A}+\angle \mathrm{B}+\angle \mathrm{C}+\angle \mathrm{D}+\angle \mathrm{E}+\angle \mathrm{F}\)
\(=540^{\circ}-180^{\circ}=360^{\circ}\) [(i) থেকে]
\(\therefore\) নির্ণেয় মান হল \(360^{\circ}\)।
WBBSE Class-8 (VIII) Koshe dekhi 16.1 WBBSE Class 8 Math Solution || ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই কষে দেখি 16.1 || WBBSE Class-8 (VIII) Koshe dekhi 16.1 Somadhan || West Bengal Board Class 8 Math Book Solution || অধ্যায় ১৬ পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদ
4. \(A B=A C\) হলে \(\angle\mathrm{ABC}, \angle \mathrm{ACB}\) ও \(\angle
\mathrm{BAC}\) –এর পরিমাপলিখি।


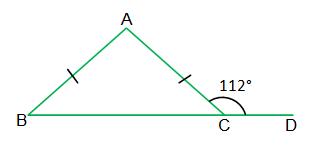
\(\triangle \mathrm{ABC}\)-এর \(AB = AC\)
\(\therefore \angle A C B=\angle A B C\)
[একটি ত্রিভুজের দুটি বাহু সমান হলে তাদের বিপরীত কোণ দুটির পরিমাপ সমান হয়]
আবার, \(\angle A C B+\angle A C D=180^{\circ}\)
বা,\(\angle A C B=180^{\circ}-\angle A C D\)
বা,\(\angle A C B=180^{\circ}-112^{\circ}=68^{\circ}\)
\(\therefore\) \(\angle A B C=68^{\circ}\)
\(\therefore\) \(\angle B A C=180^{\circ}-\left(68^{\circ}+68^{\circ}\right)=180^{\circ}-136^{\circ}=44^{\circ}\)
\(\therefore\) নির্ণেয় কোনগুলি \(\angle A B C=68^{\circ}, \angle A C B=68^{\circ}\)
\(\angle B A C=44^{\circ}\)
5. \(A B=A C\) হলে \(\angle\mathrm{ABC}\) ও \(\angle \mathrm{ACB}\) –এর পরিমাপ
লিখি।



\(\triangle \mathrm{ABC}\)-এর \(AB = AC\)
\(\therefore \angle A C B=\angle A B C\)
[একটি ত্রিভুজের দুটি বাহু সমান হলে তাদের বিপরীত কোণ দুটির পরিমাপ সমান হয়]
\(\therefore \angle \mathrm{ABC}=x\) (ধরি)
আবার, \(\angle A B C+\angle B C A+\angle B A C=180^{\circ}\)
বা, \(x+x+80^{\circ}=180^{\circ}\)
বা, \(2 x=180^{\circ}-80^{\circ}\)
বা, \(x=\frac{100^{\circ}}{2}=50^{\circ}\)
\(\therefore\) নির্ণেয় কোনগুলি \(\angle A B C=50^{\circ}, \angle A C B=50^{\circ}\)
6. \(A B=A C\) হলে \(\angle\mathrm{ACB}\) ও \(\angle \mathrm{BAC}\) –এর পরিমাপ
লিখি।
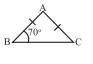


\(\triangle \mathrm{ABC}\)-এর \(\angle \mathrm{ABC}\) \(= 70^{\circ}\)
আবার, \(AB = AC\)
\(\therefore \angle A C B=\angle A B C=70^{\circ}\)
[কোনো ত্রিভুজের দুটি বাহুর দৈর্ঘ্য সমান হলে তাদের বিপরীত কোণ দুটির পরিমাপ সমান হয়।]
আবার, \(\angle A B C+\angle B A C+\angle A C B=180^{\circ}\)
বা, \(\angle B A C=180^{\circ}-\left(2 \times 70^{\circ}\right)=180^{\circ}-140^{\circ}=40^{\circ}\)
\(\therefore\) নির্ণেয় কোণগুলি \(\angle A C B=70^{\circ}, \angle B A C=40^{\circ}\)
7. \(A B=B C\) এবং \(\angle\mathrm{BAC}+\angle \mathrm{ACB}=50^{\circ} ; \Delta
\mathrm{ABC}\) –এরকোনগুলির পরিমাপ লিখি।


\(\triangle \mathrm{ABC}\)-এর \(AB = BC\)
\(\therefore \angle \mathrm{ACB}=\angle \mathrm{BAC}=x\) (ধরি)
[কোনো ত্রিভুজের দুটি বাহুর দৈর্ঘ্য সমান হলে তাদের বিপরীত কোণ দুটির পরিমাপ সমান হয়]
প্রদত্ত, \(\angle B A C+\angle A C B=50^{\circ}\)
বা, \(x+x=50^{\circ}\)
\(\therefore\) \(x=25^{\circ}\)
\(\triangle \mathrm{ABC}\)-এর
\(\angle A B C+\angle B A C+\angle B C A=180^{\circ}\)
\(\therefore \angle A B C=180^{\circ}-2 x=180^{\circ}-(2 \times 25)^{\circ} \text {. }\)
\(=180^{\circ}-50^{\circ}=130^{\circ}\)
\(\therefore\) নির্ণেয় কোনগুলি
\( \begin{array}{l} \angle A B C=130^{\circ}, \angle B A C= 25^{\circ}, \\ \quad \quad \quad \quad \quad \quad \quad\angle A C B=25^{\circ}\end{array} \)
8. \(\Delta \mathrm{ABC}\) এর অন্তঃস্থ একটি বিন্দু O; প্রমাণ করি যে
\(\angle\mathrm{BOC}>\angle \mathrm{BAC}\)

প্রদত্ত : \(\triangle \mathrm{ABC}\)-এর অন্তঃস্থ একটি বিন্দু \(O\)।
প্রামাণ্য বিষয় : \(\angle B O C>\angle B A C\)
অঙ্কন : \(BO\) বাহুকে এমনভাবে বর্ধিত করা হল যা AC বাহুকে D বিন্দুতে ছেদ করে।
প্রমাণ : আমরা জানি, ত্রিভুজের যে-কোনো বাহুকে বর্ধিত করলে উৎপন্ন বহিঃকোণ বিপরীত অন্তঃস্থ কোণের চেয়ে বড়ো হয়,
এক্ষেত্রে, \(\triangle \mathrm{DOC}\)-এর একটি বহিঃকোণ \(B\) হল
\(\angle B O C\)
\(\therefore \angle B O C>\angle O D C\)... (i)
\(\triangle \mathrm{ABD}\) -এর বহিঃকোণ \(\angle O D C>\angle B A C\) ... (ii)
\(\therefore \angle B O C>\angle B A C\) [(i) ও (ii) থেকে পাই] (প্রমাণিত)
9. প্রমাণ করি যে \(\Delta\mathrm{ABC}\) -এর BC বাহুকে উভয়দিকে বাড়ালে যে দুটি বহিঃকোণ
উৎপন্ন হয় তাদেরসমষ্টি 2 সমকোণের বেশি।

প্রদত্ত : \(ABC\) ত্রিভুজের \(BC\) বাহুকে উভয়দিকে \(P\) ও \(Q\) পর্যন্ত বর্ধিত করলে যথাক্রমে \(\triangle A B P\) ও \(\triangle A C Q\) বহিস্থ কোণ উৎপন্ন হয়।
প্রামান্য বিষয় : \(\angle A B P+\angle A C Q>2\) সমকোণ বা \(180^{\circ} \)
প্রমাণ : \(\triangle \mathrm{ABC}\)-এর ক্ষেত্রে,
বহিস্থ কোণ \(\angle \mathrm{ABP}\) = অন্তঃস্থ বিপরীত \((\angle B C A+\angle C A B)\) ... (i)
ও বহিস্থ কোণ \(\angle A C Q\)
= অন্তঃস্থ বিপরীত \((\angle \mathrm{ABC}+\angle \mathrm{CAB})\)...(ii)
[\(\because\) ত্রিভুজের কোনো একটি বাহুকে বর্ধিত করলে উৎপন্ন বহিস্থ কোণ অন্তঃস্থ বিপরীত কোণদ্বয়ের যোগফলের সমান]
(i) ও (ii) নং সমীকরণ যোগ করে পাই,
\(\angle \mathrm{ABP}+\angle \mathrm{ACQ}=\)
\(\quad \quad \quad \quad \quad (\angle \mathrm{BCA}+\angle \mathrm{CAB})+(\angle \mathrm{ABC}+\angle \mathrm{CAB})\)
বা, \(\angle \mathrm{ABP}+\angle \mathrm{ACQ}\)
\(\quad \quad \quad \quad \quad \quad \quad=(\angle \mathrm{BCA}+\angle \mathrm{CAB}+\angle \mathrm{ABC})+\angle \mathrm{CAB}\)
বা, \( \angle A B P+\angle A C Q=180^{\circ}+\angle C A B \) [\(\therefore\) ত্রিভুজের তিনটি কোণের সমষ্টি \(180^{\circ}\)]
বা, \((\angle \mathrm{ABP}+\angle \mathrm{ACQ})>180^{\circ}\)
[\(\because\) \(\angle C A B-\)-এর মান নির্দিষ্ট ধনাত্মক] (প্রমানিত)
10. \(\Delta \mathrm{ABC}\) এর কৌণিক বিন্দু A ও C দিয়ে যথাক্রমে BC ও BA
বাহুরসমান্তরাল সরলরেখা D বিন্দুতে মিলিত হয়। প্রমাণ করি যে, \(\angle\mathrm{ABC}=\angle \mathrm{ADC}\)

প্রদত্ত : \(\triangle \mathrm{ABC}\)-এর কৌণিক বিন্দু \(A \) ও \(C\) দিয়ে \(BC\) ও \(BA\) বাহুর সমান্তরাল সরলরেখাংশ D বিন্দুতে মিলিত হয়।
অর্থাৎ, \( A B \| D C \) এবং \( BC \| AD \)
প্রামাণ্য বিষয় : \(\angle A B C=\angle A D C\)
প্রমান : \( A D \| B C \) ও \(AC\) ভেদক,
\(\therefore \angle A C B=\angle D A C\) [একান্তর]
আবার, \( A B \| D C \) ও \(AC\) ভেদক হলে,
\(\angle B A C=\angle A C D\) [একান্তর]
\( \therefore \angle B A C+\angle A C B=\angle D A C+\angle D C A \) ..............(i)
\( \therefore \triangle \mathrm{ABC} \)-এর \( \angle \mathrm{ABC}=180^{\circ}-(\angle \mathrm{BAC}+\angle \mathrm{ACB}) \)
\( =180^{\circ}-(\angle \mathrm{DAC}+\angle \mathrm{DCA}) \) [(i) থেকে ]
\( =\angle \mathrm{ADC} \) (প্রমানিত)
বিকল্প প্রমাণ :
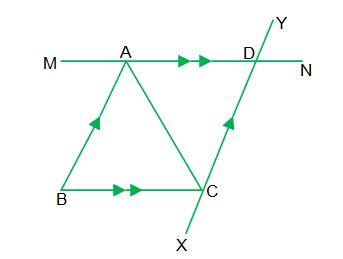
প্রদত্ত : \(\triangle \mathrm{ABC}\)-এর কৌণিক বিন্দু \(A\) ও \(C\) দিয়ে
\(BC\) ও \(BA\) বাহুর সমান্তরাল সরলরেখা যথাক্রমে \(MN\)
ও \(XY\) যারা পরস্পর \(D\) বিন্দুতে মিলিত হয়।
প্রামাণ্য বিষয় : \(\angle A B C=\angle A D C\)
প্রমাণ : \( \mathrm{MN} \| \mathrm{BC} \) এবং \(AB\) ছেদক,
\(\therefore \angle \mathrm{ABC}=\) একান্তর \(\angle \mathrm{MAB}\)....(i)
আবার \( B A \| X Y \) এবং \( MN \) ছেদক
\(\therefore\) \(\angle \mathrm{MAB}\). = অনুরূপ \(\angle \mathrm{ADC}\)....(ii)
\(\therefore\) (i) ও (ii) থেকে পাই,
\(\angle A B C=\angle A D C\)
\([\because \angle \mathrm{ABC}\) এবং \(\mathrm{ADC}\) উভয়েই \( \angle M A B \)-এর সমান ]
11. \(\Delta \mathrm{ABC}\) এর \(\angle \mathrm{ABC}\) ও \(\angle\mathrm{ACB}\) এর
অন্তঃসমদ্বিখণ্ডকদ্বয় O বিন্দুতে মিলিত হয়। প্রমাণ করি যে,\(\angle B O C=90^{\circ}+\frac{1}{2} \angle B
A C\)

প্রদত্ত : \( \triangle A B C \)-এর \( \angle A B C \) ও
\( \angle A C B \)-এর অন্তঃসমদ্বিখণ্ডকদ্বয় \(O\) বিন্দুতে মিলিত হয়েছে।
প্রামাণ্য বিষয় : \( \angle B O C=90^{\circ}+\frac{1}{2} \angle B A C \)
প্রমান : \( \triangle \mathrm{ABC}\) -এর, \( \angle \mathrm{ABC}+\angle \mathrm{BCA}+\angle \mathrm{BAC}=180^{\circ} \)
বা, \( \frac{1}{2} \angle A B C+\frac{1}{2} \angle B C A+\frac{1}{2} \angle B A C=\frac{1}{2} \times 180^{\circ}=90^{\circ}\)
বা, \(\frac{1}{2} \angle A B C+\frac{1}{2} \angle B C A=90^{\circ}-\frac{1}{2} \angle B A C \) ............(i)
আবার \( \triangle \mathrm{BOC} \) থেকে,
\( \angle \mathrm{BOC}+\angle \mathrm{OBC}+\angle \mathrm{OCB}=180^{\circ}\)
বা, \(\angle \mathrm{BOC}+\frac{1}{2} \angle \mathrm{ABC}+\frac{1}{2} \angle \mathrm{BCA}=180^{\circ} \)
[যেহেতু, \(BO, \angle A B C \)-এর এবং , \( CO\angle B C A \) এর সমদ্বিখণ্ডক]
বা, \( \frac{1}{2} \angle \mathrm{ABC}+\frac{1}{2} \angle \mathrm{BCA}=180^{\circ}-\angle \mathrm{BOC} \).... (ii)
(i) ও (ii) থেকে পাই, \( 90^{\circ}-\frac{1}{2} \angle B A C=180^{\circ}-\angle B O C \)
বা, \( \angle B O C=180^{\circ}-90^{\circ}+\frac{1}{2} \angle B A C \)
\( =90^{\circ}+\frac{1}{2} \angle \mathrm{BAC} \) (প্রমাণিত)
WBBSE Class-8 (VIII) Koshe dekhi 16.1 WBBSE Class 8 Math Solution || ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই কষে দেখি 16.1 || WBBSE Class-8 (VIII) Koshe dekhi 16.1 Somadhan || West Bengal Board Class 8 Math Book Solution || অধ্যায় ১৬ পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদ
12. \(\Delta A B C\) –এর \(\angle \mathrm{ABC}\) ও \(\angle \mathrm{ACB}\)
এরবহিঃসমদ্বিখণ্ডকদ্বয় O বিন্দুতে মিলিত হয়। প্রমাণ করি যে, \(\angle\mathrm{BOC}=90^{\circ}-\frac{1}{2}
\angle \mathrm{BAC}\)
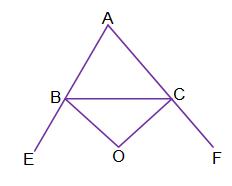
প্রদত্ত : \( \triangle A B C \)-এর \( \angle A B C \)
ও \( \angle A C B\) বর্হিসমদ্বিখণ্ডকদ্বয় \(O\) বিন্দুতে ছেদ করে।
প্রামাণ্য বিষয় :
\( \angle B O C=90^{\circ}-\frac{1}{2} \angle B A C \)
প্রমাণ : \( \angle \mathrm{ABC}+\angle \mathrm{CBE}=180^{\circ} \)...(i)
কিন্তু \( \angle \mathrm{CBE}- \)এর অন্তঃসমদ্বিখণ্ডক \(BO\)
\( \therefore \angle O B E=\angle O B C \)
অর্থাৎ,\( \angle \mathrm{CBE}=2 \angle \mathrm{CBO} \)
\(\therefore\) (i) থেকে পাই,
\( \angle \mathrm{ABC}+2 \angle \mathrm{CBO}=180^{\circ} \)
বা, \( \angle \mathrm{CBO}=\frac{1}{2}\left(180^{\circ}-\angle \mathrm{ABC}\right)=90^{\circ}-\frac{1}{2} \angle \mathrm{ABC} \ldots \) (ii)
আবার \( \angle \mathrm{ACF}=1 \) সরলকোণ
\( \therefore \angle \mathrm{ACB}+\angle B C F=180^{\circ} \ldots\) (iii)
কিন্তু, \( \angle B C F \)-এর অন্তঃসমদ্বিখণ্ডক CO
\( \therefore \angle B C O=\angle O C F \) অর্থাৎ, \( \angle B C F=2 \angle B C O \)
\( \therefore \) (iii) থেকে পাই \( \angle \mathrm{ACB}+2 \angle \mathrm{BCO}=180^{\circ} \)
বা, \( \angle B C O=\frac{1}{2}\left(180^{\circ}-\angle A C B\right)=90^{\circ}-\frac{1}{2} \angle A C B \ldots \) (iv)
এখন \( \triangle B O C \) থেকে পাই,
\( \angle B O C=180^{\circ}-\angle C B O-\angle B C O \) \( \left[\because \angle B O C+\angle O B C+\angle B C O=180^{\circ}\right] \)
\( \begin{array}{l}=180^{\circ}-\left(90^{\circ}-\frac{1}{2} \angle \mathrm{ABC}\right)-\left(90^{\circ}-\frac{1}{2} \angle \mathrm{ACB}\right) \\ =180^{\circ}-90^{\circ}-90^{\circ}+\frac{1}{2} \angle \mathrm{ABC}+\frac{1}{2} \angle \mathrm{ACB} \\ =\frac{1}{2}(\angle \mathrm{ABC}+\angle \mathrm{ACB})=\frac{1}{2}\left(180^{\circ}-\angle \mathrm{BAC}\right)\end{array} \)
\( =90^{\circ}-\frac{1}{2} \angle B A C \) (প্রমানিত)
13. \(\Delta \mathrm{ABC}\) –এর \(\angle \mathrm{ACB}\) -এর বহিঃসমদ্বিখণ্ডক Aবিন্দু
দিয়ে BC বাহুর সমান্তরাল সরলরেখাকে D বিন্দুতে ছেদ করে। প্রমাণ করি যে,\(\angle
\mathrm{ADC}=90^{\circ}-\frac{1}{2} \angle \mathrm{ACB}\)

প্রদত্ত : \(ABC\) ত্রিভুজের \(BC\) বাহুকে \(E\) পর্যন্ত বর্ধিত করা হল।
\(CD\) সরলরেখা \( \angle {ACE} \) কে সমদ্বিখণ্ডিত করে।
\(A\) বিন্দু দিয়ে অঙ্কিত \(BC\)-এর সমান্তরাল সরলরেখা
\( \angle {ACE} \)-এর সমদ্বিখণ্ডককে \(D\) বিন্দুতে ছেদ করে।
প্রামাণ্য বিষয় : \( \angle \mathrm{ADC}=90^{\circ}-\frac{1}{2} \angle \mathrm{ACB} \)
প্রমাণ : \( \angle \mathrm{ACB}+\angle \mathrm{ACE}=180^{\circ} \) [BC রেখাংশের উপর C বিন্দুতে CF রেখাংশ দণ্ডায়মান হওয়ায় সন্নিহিত কোণদ্বয়ের সমষ্টি 180°]
\( \therefore \angle A C E=180^{\circ}-\angle A C B \) ...(i)
\( \angle A C E \)-এর অন্তঃসমদ্বিখণ্ডক CD
\( \therefore \angle A C D=\angle D C E \)
বা, \( \angle \mathrm{DCE}=\frac{1}{2} \angle \mathrm{ACE} \)
\( =\frac{1}{2}\left(180^{\circ}-\angle \mathrm{ACB}\right)\)
\(=90^{\circ}-\frac{1}{2} \angle \mathrm{ACB} \).............(ii)
আবার \( X Y \| B E \) এবং \(FC\) ছেদক
\( \angle \mathrm{ADC}= \) একান্তর \( \angle \mathrm{DCE} \)
বা, \( \angle \mathrm{ADC}=90^{\circ}-\frac{1}{2} \angle \mathrm{ACB} \) [(ii) নং থেকে] (প্রমাণিত)
বিকল্প প্রমাণ :

\( A D \| B C, A C \) ভেদক,
\( \therefore \angle D A C= \) একান্তর \( \angle \mathrm{ACB} \)
\( \triangle \mathrm{ABC} \)-এর,
\( \angle \mathrm{ABC}+\angle \mathrm{CAB}+\angle \mathrm{ACB}=2 \) সমকোণ
\( \therefore \frac{1}{2}(\angle \mathrm{ABC}+\angle \mathrm{CAB}+\angle \mathrm{ACB})\)
\(=2 \times \frac{1}{2}\) সমকোণ \(= 1\) সমকোণ
\( \triangle \mathrm{ABC}- \)এর, বহিঃকোণ \( \angle A C E \)
= অন্তঃস্থ বিপরীত \( (\angle \mathrm{ABC}+\angle \mathrm{BAC}) \)
আবার, \( \angle D C A=\frac{1}{2} \angle A C E \)
\( \therefore \angle D C A=\frac{1}{2}(\angle B A C+\angle A B C) \)
\( \triangle \mathrm{ADC}\)-এ র, \(\angle \mathrm{ADC}+\angle \mathrm{ACD}+\angle \mathrm{DAC}=180^{\circ} \)
\( \begin{array}{l}=180^{\circ}-\frac{1}{2}(\angle B A C+\angle A B C)-\angle A C B \\ =180^{\circ}-\frac{1}{2}(\angle B A C+\angle A B C+\angle A C B)-\frac{1}{2} \angle A C B \\ =180^{\circ}-\frac{1}{2} \times 180^{\circ} -\frac{1}{2} \angle A C B\end{array} \)
\( \left[\because \triangle \mathrm{ABC}\right. \)-এর তিনটি কোণের সমষ্টি \( \left.180^{\circ}\right] \)
\( =180^{\circ}-90^{\circ}-\frac{1}{2} \angle A C B \)
\( =90^{\circ}-\frac{1}{2} \angle A C B \)
\( \therefore \angle A D C=90^{\circ}-\frac{1}{2} \angle A C B \) প্রমানিত
14. প্রমাণ করি যে, একটি ত্রিভুজের শীর্ষকোণের সমদ্বিখণ্ডক এবং শীর্ষকোণ থেকেভূমির উপর
অঙ্কিত লম্বের অন্তর্ভুক্ত কোণ ত্রিভুজের ভূমিস্থ কোণদ্বয়ের অন্তরেরঅর্ধেক।

ধরা যাক \( \triangle \mathrm{ABC} \)-এর শীর্ষকোণ \( \angle B A C \)
-এর সমদ্বিখণ্ডক \(AE, BC\) বাহুকে \(E\) বিন্দুতে এবং \(BC\) বাহুর উপর
\( AD\) লম্বটি \(BC\)-কে \(D\) বিন্দুতে ছেদ করে
এবং \( \angle C>\angle B \)
প্রামাণ্য বিষয় : \( \angle E A D=\frac{1}{2}(\angle C-\angle B) \)
প্রমাণ :
\( \because A E, \angle B A C \)-এর সমদ্বিখণ্ডক,
\( \therefore \angle B A E=\angle E A C \).........................(i)
\( \triangle \mathrm{ACD} \) সমকোণী ত্রিভুজ থেকে পাই -
\( \angle A C D=90^{\circ}-\angle C A D\left[\because \angle D=90^{\circ}\right]\).................... (ii)
আবার সমকোণী ত্রিভুজ ABD থেকে পাই –
\( \angle A B D=90^{\circ}-\angle B A D\left[\because \angle D=90^{\circ}\right] \).................... (iii)
(ii) - (iii) করে, \( \angle A C D-\angle A B D \)
\( =\left(90^{\circ}-\angle C A D\right)-\left(90^{\circ}-\angle B A D\right)\)
\(=90^{\circ}-\angle C A D-90^{\circ}+\angle B A D\)
\(=\angle B A D-\angle C A D\)
\(=(\angle B A E+\angle E A D)-(\angle C A E-\angle E A D)[\text { [চিত্রানুসারে }]\)
\(=\angle B A E+\angle E A D-\angle C A E+\angle E A D\)
\(=2 \angle \mathrm{EAD}[\because \angle B A E=\angle C A E] \)
অর্থাৎ, 2 \( \angle \mathrm{EAD}=\angle \mathrm{ACD}-\angle \mathrm{ABD} \)
বা, \( \angle E A D=\frac{1}{2}(\angle A C D-\angle A B D) \)
\( \therefore \angle E A D=\frac{1}{2}(\angle C-\angle B) \) (প্রমানিত)
15. ABC সমদ্বিবাহু ত্রিভুজের ভূমির একটি কোণ শীর্ষকোণের দ্বিগুণ। ত্রিভুজটিরকোণগুলির
পরিমাপ লিখি।
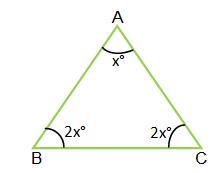
প্রদত্ত : মনে করি,
\( \triangle \mathrm{ABC} \)-এর \(AB = AC\), শীর্ষকোণ \(= x^{\circ}\) \( \angle A B C=2 x^{\circ} \)
আবার \(AB = AC\),
\( \therefore \angle A B C=\angle A C B=2 x^{\circ} \)
\( \triangle \mathrm{ABC}\)-এর, \(\angle \mathrm{ABC}+\angle \mathrm{ACB}+\angle \mathrm{BAC}=180^{\circ} \)
বা, \( 2 x^{\circ}+2 x^{\circ}+x^{\circ}=180^{\circ}\)
বা, \(5 x^{\circ}=180^{\circ}\)
বা, \(x^{\circ}=\frac{180^{\circ}}{5}=36^{\circ} \)
\( \therefore \quad x^{\circ}=36^{\circ} \) এবং \( 2 x^{\circ}=2 \times 36^{\circ}=72^{\circ} \)
\(\therefore\) সমদ্বিবাহু ত্রিভুজের নির্ণেয় কোণগুলির পরিমাপ হল \(36^{\circ}, 72^{\circ}, 72^{\circ} \)।
16. \(\Delta \mathrm{ABC}\)-এর \(\angle \mathrm{BAC}=90^{\circ}\) এবং \(\angle
\mathrm{BCA}=30^{\circ}\);প্রমাণ করি যে, \(A B=\frac {1}{2} B C\).

প্রদত্ত : \( \triangle A B C \)-এর \( \angle B A C=90^{\circ} \) এবং \( \angle B C A=30^{\circ} \)
প্রামাণ্য বিষয় : \( A B=\frac{1}{2} B C \)
অঙ্কন : \(BA\) বাহুকে \(D\) বিন্দু পর্যন্ত এমনভাবে বর্ধিত করা হল
যাতে \(BA = AD\) হয়। \(C, D\) যুক্ত করা হল।
প্রমাণ : \( \triangle B A C\) ও \(\triangle D A C- \)এর
(i) \( BA = DA\) [অঙ্কনানুসারে]
(ii) \( \angle B A C=\angle D A C=90^{\circ} \) [প্রদত্ত]
(iii) \(AC\) উভয় ত্রিভুজের সাধারণ বাহু
\( \therefore \triangle \mathrm{BAC} \cong \triangle \mathrm{DAC} \) [SAS সর্বসমতা অনুসারে]
\( \therefore \angle A C B=\angle A C D \) [সর্বসম ত্রিভুজের অনুরূপ কোণ]
\( \therefore \angle A C D=30^{\circ}\left[\because \angle A C B=30^{\circ}\right. \) (প্রদত্ত) )
\( \begin{aligned} \therefore \quad & \angle B C D=\angle A C B+\angle A C D=30^{\circ}+30^{\circ}=60^{\circ} \\ & \triangle B A C-এ র, \angle B A C+\angle A C B+\angle C B A=180^{\circ}\end{aligned} \)
বা, \( 90^{\circ}+30^{\circ}+\angle C B A=180^{\circ}\)
বা, \(\angle C B A=180^{\circ}-\left(90^{\circ}+30^{\circ}\right)=180^{\circ}-120^{\circ}=60^{\circ}\)
বা, \(\angle C B D=60^{\circ} \)
আবার, \( \angle C B A=\angle C D A \)
[সর্বসম ত্রিভুজের অনুরূপ কোণ]
\( \therefore \angle \mathrm{CDA}=60^{\circ}\left[\because \angle \mathrm{CBA}=60^{\circ}\right] \)
বা, \( \angle \mathrm{BDC}=60^{\circ} \)
\( \therefore \triangle \mathrm{BDC}\)-এ র \(\angle C B D=\angle \mathrm{CDB}=\angle \mathrm{BCD}=60^{\circ} \)
\( \therefore \triangle \mathrm{BDC} \) সমবাহু ত্রিভুজ যার \(BD = DC = BC\)
\(BD\)-এর মধ্যবিন্দু \(A\) [অঙ্কনানুসারে]
অর্থাৎ, \( A B=\frac{1}{2} B D \)
বা, \( A B=\frac{1}{2} B C[\because B D=B C] \) (প্রমাণিত)
বিকল্প পদ্ধতিঃ

অঙ্কন : \(BC\) থেকে \(BA\)-এর সমান করে \(BD\) অংশ কেটে নেওয়া \(B\) হল। \( A, D\) যুক্ত করা হল।
প্রমাণ : \( \triangle \mathrm{ABC} \)-এর \( \angle C=30^{\circ} \)
\( \therefore \angle A B C=180^{\circ}-\left(90^{\circ}+30^{\circ}\right) \)
\( =60^{\circ}=\angle \mathrm{ABD} \)
আবার \(AB = BD\) (অঙ্কনানুসারে)
\( \therefore \angle B A D=\angle B D A=\frac{1}{2}\left(180^{\circ}-60^{\circ}\right)=\frac{1}{2} \times 120^{\circ}=60^{\circ} \)
\( \therefore \quad \triangle B A D \) একটি সমবাহু ত্রিভুজ। \(AB = BD = AD\) ... (i)
আবার, \( \triangle \mathrm{ADC}-এ র ~ \angle A D C=180^{\circ}-\angle A D B \)
\( =180^{\circ}-60^{\circ}=120^{\circ} \)
\( \therefore \angle D A C=180^{\circ}-\left(120^{\circ}+30^{\circ}\right)=180^{\circ}-150^{\circ}=30^{\circ} \)
সুতরাং \( \angle D A C=\angle D C A \)
\(\therefore\) \(DC = AD\) ... (ii)
(i) ও (ii) থেকে পাই, \(AB = BD = DC\)
\( \therefore A B=\frac{1}{2} B C \) (প্রমাণিত)
17. \(\Delta \mathrm {X Y Z}\) –এর \(\angle \mathrm{XYZ}=90^{\circ}\) এবং\(\mathrm{X
Y}=\frac{1}{2}\mathrm{X Z}\); প্রমাণ করি যে, \(\angle\mathrm{YXZ}=60^{\circ}\)

প্রদত্ত : \( \Delta \mathrm{XYZ} \)-এর \( \angle X Y Z=90^{\circ} \) এবং \( X Y=\frac{1}{2} X Z \)
প্রামাণ্য বিষয় : \( \angle Y X Z=60^{\circ} \)
অঙ্কন : \(XY\) বাহুকে \(P\) বিন্দু পর্যন্ত এমনভাবে বর্ধিত করা হল,
যাতে \(XY = YP\) হয়। \(P, Z\) যুক্ত করা হল।
প্রমাণ : \( \triangle X Y Z \) ও \( \triangle P Y Z \) -এর
(i) \(XY = PY\) [অঙ্কনানুসারে]
(ii) \( \angle \mathrm{XYZ}=\angle \mathrm{PYZ}=90^{\circ} \) [প্রদত্ত]
(iii) \(YZ = YZ\) [সাধারণ বাহু]
\( \therefore \Delta X Y Z \cong \triangle P Y Z \) [SAS শর্তানুযায়ী]
\(\therefore\) \(XZ = PZ\) [সর্বসম ত্রিভুজের অনুরূপ বাহু] ...............(i)
\(\therefore\) \(XP\) বাহুর মধ্যবিন্দু \(Y\) [\(\because\) \(XY = YP \) (অঙ্কনানুসারে)]
বা, \( X Y=\frac{1}{2} X P\)
বা, \(\frac{1}{2} X Z=\frac{1}{2} X P\left[\because X Y=\frac{1}{2} X Z\right]\)
বা, \(X Z=X P \).....................(ii)
(i) ও (ii) থেকে পাই, \(XZ = PZ = XP\)
\( \therefore \triangle P X Z \) সমবাহু।
\( \therefore \angle P X Z=60^{\circ} \)
বা, \( \angle \mathrm{Y} X Z=60^{\circ} \) (প্রমানিত)
বিকল্প পদ্ধতি :
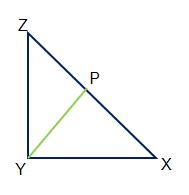
অঙ্কন : \( \angle Z \)-এর সমান করে \(Y\) বিন্দুতে \( \angle Z Y P \)
অঙ্কন করা হল, \(YP \quad ZX\)-কে \(P\) বিন্দুতে ছেদ করল।
প্রমাণ : যেহেতু \( \angle P Y Z=\angle P Z Y \)
\( \therefore \mathrm{PY}=\mathrm{PZ} \)
এখন, \( \angle P Y Z+\angle P Y X=\angle P X Y+\angle P Z Y=90^{\circ} \)
\( \begin{array}{l}\therefore \angle P Y X=\angle P X Y ~[\because \angle P Y Z=P Z Y] \\ \therefore P X=P Y \therefore P X=P Y=P Z\end{array} \)
\(\therefore\) \(P, ZX\)-এর মধ্যবিন্দু এবং \( P Y=\frac{1}{2} X Z \)
কিন্তু \( X Y=\frac{1}{2} X Z \)
\( \therefore \mathrm{PY}=\mathrm{XY}=\mathrm{PX} \)
\(\therefore \triangle \mathrm{PXY} \) সমবাহু ত্রিভুজ।
\( \therefore \angle Y X P=\angle Y X Z=60^{\circ} \) (প্রমানিত)
18. প্রমাণ করি যে, সমবাহু ত্রিভুজের প্রতিটি কোণের পরিমাপ \(60^{\circ}\)

ধরা যাক, \( \triangle \mathrm{ABC} \) সমবাহু ত্রিভুজ
অর্থাৎ,\( AB = BC = CA\)
প্রামাণ্য বিষয় : \( \angle A=\angle B=\angle C=60^{\circ} \)
প্রমাণ : \( \triangle \mathrm{ABC} \)-এর \(AB = AC\)
\( \therefore \angle C=\angle B \)...................(i)
আবার \( B C=B A \)
\(\therefore \angle A=\angle C \ldots \) (ii)
এবং \( \mathrm{CA}=\mathrm{CB} \)
\(\therefore \angle \mathrm{B}=\angle \mathrm{A} \).................(iii)
(i), (ii), (iii) থেকে,
\( \angle \mathrm{A}=\angle \mathrm{B}=\angle \mathrm{C} \ldots(iv) \)
\( \because \triangle A B C\)-এর \(\angle A+\angle B+\angle C=180^{\circ} \)
বা, \( \angle \mathrm{A}+\angle \mathrm{A}+\angle \mathrm{A}=180^{\circ}\)
বা, \(3 \angle \mathrm{A}=180^{\circ}\)
বা, \(\angle \mathrm{A}=\frac{180^{\circ}}{3^{\circ}}=60^{\circ} \)
\( \therefore \angle \mathrm{A}=\angle \mathrm{B}=\angle \mathrm{C}=60^{\circ} \) (প্রমানিত)
19. ABC ত্রিভুজের \(\angle \mathrm{BAC}\) -এর সমদ্বিখণ্ডক এবং AC বাহুরমধ্যবিন্দু D
দিয়ে AB বাহুর সমান্তরাল সরলরেখা পরস্পর BC বাহুর বাইরে E বিন্দুতেমিলিত হয়। প্রমাণ করি যে, \(\angle
\mathrm{AEC}=1\) সমকোণ।

প্রদত্ত : \(ABC\)-এর \( \angle B A C \)-এর সমদ্বিখণ্ডক
এবং \(AC\) বাহুর মধ্যবিন্দু \(D\) দিয়ে \(AB\) বাহুর সমান্তরাল করে
\(DE\) সরলরেখা অঙ্কন করা হল যা পরস্পরকে BC বাহুর
বাইরে \(E\) বিন্দুতে মিলিত হয়। \(E, C\) যুক্ত করা হল।
প্রামাণ্য বিষয় : \( \angle A E C = 1\) সমকোণ
প্রমাণ : \( A B \| D E \) এবং \(AE\) ভেদক
\( \angle \mathrm{BAE}=\angle \mathrm{AED}=x^{\circ} \) (ধরি)
আবার \( \angle B A C\)-এর সমদ্বিখণ্ডক \(AE \)
\(\angle \mathrm{BAE} =\angle \mathrm{EAC}=x^{\circ}\)
\(\therefore \angle \mathrm{DAE} =\angle \mathrm{AED}=x^{\circ} \)
\(\therefore \mathrm{AD}=\mathrm{DE}\).............(i)
এখন, \( \triangle \mathrm{ADE} \)-এর বহিঃকোণ \( E D C \)= অন্তঃস্থ বিপরীত
কোণ \( (\angle \mathrm{DAE}+\angle \mathrm{AED})=x^{\circ}+x^{\circ}=2 x^{\circ} \)
আবার \(D, AC\)-এর মধ্যবিন্দু
\(\therefore\) \(AD = DC\)
\(\therefore\) \(ED = DC\)
সুতরাং \( \angle \mathrm{DCE}=\angle \mathrm{DEC} \)
কিন্তু \( \Delta \mathrm{DCE}\) -এর \(\angle \mathrm{DEC}+\angle \mathrm{DCE}+\angle \mathrm{EDC}=180^{\circ} \)
বা, \( \angle \mathrm{DCE}+\angle \mathrm{DEC}=180^{\circ}-\angle \mathrm{EDC}\)
বা, \(2 \angle \mathrm{DEC}=180^{\circ}-2 x^{\circ}[\because \angle \mathrm{AED}=\angle \mathrm{DCE}]\)
বা, \(\angle \mathrm{DEC}=90^{\circ}-x \ldots \text { (ii) } \)
\( \begin{array}{l}\text { এখন } \angle \mathrm{AEC}=\angle \mathrm{AED}+\angle \mathrm{DEC} \quad\left[\because \angle \mathrm{AED}=x^{\circ}\right] \\ =x^{\circ}+90^{\circ}-x^{\circ}\end{array} \)
\( =90^{\circ}=1 \) সমকোণ (প্রমানিত)
WBBSE Class-8 (VIII) Koshe dekhi 16.1 WBBSE Class 8 Math Solution || ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই কষে দেখি 16.1 || WBBSE Class-8 (VIII) Koshe dekhi 16.1 Somadhan || West Bengal Board Class 8 Math Book Solution || অধ্যায় ১৬ পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদ
এই Page টি বা এই Website টির কোন প্রকার বিষয়বস্তু কপি করা বা সম্পাদনা করা নিষিদ্ধ। ভারতীয় Copywright আইন
1957 এর ধারা 63 অনুযায়ী, এই ফাইলটির সমস্ত অধিকার 'ছাত্র মিত্র Mathematics' অ্যাপ দ্বারা সংরক্ষিত। ছাত্র
মিত্রের অনুমতি ছাড়া, এই Page টি বা এই Website টির কোন প্রকার বিষয়বস্তু কপি করা বা সম্পাদনা করা আইনত
দন্ডনীয় অপরাধ। কেউ ছাত্র মিত্রের অনুমতি ছাড়া, এই Page টি বা এই Website টির কোন প্রকার বিষয়বস্তু কপি বা
সম্পাদনা করলে ছাত্র মিত্র কতৃপক্ষ তার বিরুদ্ধে সকল প্রকার কঠোর আইনি পদক্ষেপ করবে।
West Bengal Board of Secondary Education Official Site
Class 8 : গণিত প্রভা (অষ্টম শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali.
Class 7 : গণিত প্রভা (সপ্তম শ্রেণি) বইয়ের সমস্ত সমাধান
www.wbresults.nic.in Official
Class 10 : মাধ্যমিক গণিত প্রকাশ (দশম শ্রেণি) বইয়ের সমস্ত সমাধান Class 10 Maths Solution WBBSE Bengali
Class 6 : গণিত প্রভা (ষষ্ঠ শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali
Class 9 : গণিত প্রকাশ (নবম শ্রেণি) বইয়ের সমাধান Maths Solution WBBSE Bengali
আজই Install করুন Chatra Mitra
Class 8 : গণিত প্রভা (অষ্টম শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali.
Class 7 : গণিত প্রভা (সপ্তম শ্রেণি) বইয়ের সমস্ত সমাধান
www.wbresults.nic.in Official
Class 10 : মাধ্যমিক গণিত প্রকাশ (দশম শ্রেণি) বইয়ের সমস্ত সমাধান Class 10 Maths Solution WBBSE Bengali
Class 6 : গণিত প্রভা (ষষ্ঠ শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali
Class 9 : গণিত প্রকাশ (নবম শ্রেণি) বইয়ের সমাধান Maths Solution WBBSE Bengali
আজই Install করুন Chatra Mitra



