গণিত প্রকাশ সমাধান নবম শ্রেণী || গণিত প্রকাশ রাশিবিজ্ঞান (Class-9) কষে দেখি 11.2 || West Bengal Board Class 9 Math Solution Chapter 11 || Class 9 Solution koshe dekhi 11.2 || রাশিবিজ্ঞান || WBBSE Class 9 Math koshe dekhi 11.2 || Ganit Prakash Class 9 Solution koshe dekhi 11.2 || Ganit Prakash Solution Class 9 In Bengali || West Bengal Board Class 9 Math Solution Chapter 11 রাশিবিজ্ঞান
Share this page using :
গণিত প্রকাশ সমাধান নবম শ্রেণী || গণিত প্রকাশ রাশিবিজ্ঞান || Class 9 Chapter 11 || Ganit Prakash Class 9 Math Solution || West Bengal Board Class 9 Math || Class 9 Chapter 11 koshe dekhi 11.2 || নবম শ্রেণী কষে দেখি 11.2 || রাশিবিজ্ঞান
কষে দেখি - 11.2
গণিত প্রকাশ সমাধান নবম শ্রেণী || গণিত প্রকাশ রাশিবিজ্ঞান || Class 9 Chapter 11 || Ganit Prakash Class 9 Math Solution || West Bengal Board Class 9 Math || Class 9 Chapter 11 koshe dekhi 11.2 || নবম শ্রেণী কষে দেখি 11.2 || রাশিবিজ্ঞান
1. বকুলতলা গ্রামের 50টি দোকানের দৈনিক লাভ (টাকায়) নীচের ছক করে লিখলাম-
\(\begin{array}{|c|c|c|c|c|c|}
\hline \text { দৈনিক লাভ (Rs.) } & 0-50 & 50-100 & 100-150 & 150-200 & 200-250 \\
\hline \text { দোকানের সংখ্যা } & 8 & 15 & 10 & 12 & 5 \\
\hline
\end{array}\)
\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 1 বাহুকে 5 একক এবং Y অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহুকে 1 একক ধরে প্রদত্ত তথ্যের আয়তলেখ করা হল।

\hline \text { দৈনিক লাভ (Rs.) } & 0-50 & 50-100 & 100-150 & 150-200 & 200-250 \\
\hline \text { দোকানের সংখ্যা } & 8 & 15 & 10 & 12 & 5 \\
\hline
\end{array}\)
\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 1 বাহুকে 5 একক এবং Y অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহুকে 1 একক ধরে প্রদত্ত তথ্যের আয়তলেখ করা হল।

2. মিতা তাদের স্কুলের 75 জন বন্ধুদের উচ্চতা মেপে নীচের ছকে লিখল।
\(\begin{array}{|c|c|c|c|c|c|}
\hline \text { উচ্চতা (সেমি) } & 136-142 & 142-148 & 148-154 & 154-160 & 160-166 \\
\hline \text { বন্ধুদের সংখ্যা } & 12 & 18 & 26 & 14 & 05 \\
\hline
\end{array}\)
\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহুকে 1 একক এবং Y অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহুকে 1 একক ধরা হল। মিতার সংগৃহীত তথ্যের আয়তলেখটি নিম্নরূপ :

\hline \text { উচ্চতা (সেমি) } & 136-142 & 142-148 & 148-154 & 154-160 & 160-166 \\
\hline \text { বন্ধুদের সংখ্যা } & 12 & 18 & 26 & 14 & 05 \\
\hline
\end{array}\)
\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহুকে 1 একক এবং Y অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহুকে 1 একক ধরা হল। মিতার সংগৃহীত তথ্যের আয়তলেখটি নিম্নরূপ :

3. আমাদের পাড়ার 10 বছর থেকে বছর 45 বয়স পর্যন্ত বাসিন্দাদের মধ্যে হিন্দিভাষীলোকের সংখ্যা সংগ্রহ করে নীচের ছকে লিখলাম।
প্রদত্ত পরিসংখ্যা বিভাজন ছকটি বিচ্ছিন্ন (discontinuous) পরিসংখ্যা বিভাজন ছক। প্রথমে প্রদত্ত বিচ্ছিন্ন পরিসংখ্যা বিভাজন ছককে নিম্নে অবিচ্ছিন্ন পরিসংখ্যা বিভাজন ছকে পরিণত করা হল।
\(\begin{array}{|c|c|c|c|c|c|c|}
\hline \text { শ্রেণি বিভাগ } & 9.5-15.5 & 15.5-21.5 & 21.5-27.5 & 27.5-33.5 & 33.5-39.5 & 39.5-45.5\\
\hline \text { পরিসংখ্যা } & 8 & 14 & 10 & 20 & 6 & 12 \\
\hline
\end{array}\)
\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহুকে 1 একক এবং Y অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহুকে 1 একক ধরে প্রদত্ত তথ্যের আয়তলেখ অঙ্কিত হল।

\(\begin{array}{|c|c|c|c|c|c|c|}
\hline \text { শ্রেণি বিভাগ } & 9.5-15.5 & 15.5-21.5 & 21.5-27.5 & 27.5-33.5 & 33.5-39.5 & 39.5-45.5\\
\hline \text { পরিসংখ্যা } & 8 & 14 & 10 & 20 & 6 & 12 \\
\hline
\end{array}\)
\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহুকে 1 একক এবং Y অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহুকে 1 একক ধরে প্রদত্ত তথ্যের আয়তলেখ অঙ্কিত হল।

4. নীচের পরিসংখ্যা বিভাজন ছকটির আয়তলেখ অঙ্কন করি :
প্রদত্ত পরিসংখ্যা বিভাজন ছকটি বিচ্ছিন্ন (discontinuous) পরিসংখ্যা বিভাজন ছক। প্রথমে প্রদত্ত বিচ্ছিন্ন পরিসংখ্যা বিভাজন ছককে নিম্নে অবিচ্ছিন্ন পরিসংখ্যা বিভাজন ছকে পরিণত করা হল।
\(\begin{array}{|c|c|c|c|c|c|c|}
\hline \text { শ্রেণি } & 0.5-10.5 & 10.5-20.5 & 20.5-30.5 & 30.5-40.5 & 40.5-50.5 & 50.5-60.5\\
\hline \text { পরিসংখ্যা } & 8 & 3 & 6 & 12 & 2 & 7 \\
\hline
\end{array}\)
\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহুকে = 1 একক এবং Y-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহুকে = 1 একক ধরে প্রদত্ত তথ্যের আয়তলেখ অঙ্কিত হল।

\(\begin{array}{|c|c|c|c|c|c|c|}
\hline \text { শ্রেণি } & 0.5-10.5 & 10.5-20.5 & 20.5-30.5 & 30.5-40.5 & 40.5-50.5 & 50.5-60.5\\
\hline \text { পরিসংখ্যা } & 8 & 3 & 6 & 12 & 2 & 7 \\
\hline
\end{array}\)
\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহুকে = 1 একক এবং Y-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহুকে = 1 একক ধরে প্রদত্ত তথ্যের আয়তলেখ অঙ্কিত হল।

গণিত প্রকাশ সমাধান নবম শ্রেণী || গণিত প্রকাশ রাশিবিজ্ঞান || Class 9 Chapter 11 || Ganit Prakash Class 9 Math Solution || West Bengal Board Class 9 Math || Class 9 Chapter 11 koshe dekhi 11.2 || নবম শ্রেণী কষে দেখি 11.2 || রাশিবিজ্ঞান
5. পৃথাদের স্কুলের 75 জন শিক্ষার্থীদের নিম্নলিখিত প্রাপ্ত নম্বরের পরিসংখ্যা বহুভুজ অঙ্কন করি।
প্রদত্ত পরিসংখ্যা বিভাজনের পরিসংখ্যা বহুভুজ অঙ্কনের জন্য প্রথমে নীচের ছক প্রস্তুত করা হল।

(i) \(X\)-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের একবাহু = 1 একক এবং
(ii) Y-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের পাঁচ বাহুর দৈর্ঘ্য = 1 একক ধরা হল।
উপরে বর্ণিত স্কেল অনুযায়ী A (20, 0), B (30, 12), C (40, 18), D (50, 21), E (60, 15), F (70, 6), G (80, 3) ও H (90, 0) বিন্দুগুলি স্থাপন করে এবং পরপর বিন্দুগুলিকে সরলরেখাংশ দ্বারা যুক্ত করে ABCDEFGH পরিসংখ্যা বহুভুজ অঙ্কন করা হল।


(i) \(X\)-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের একবাহু = 1 একক এবং
(ii) Y-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের পাঁচ বাহুর দৈর্ঘ্য = 1 একক ধরা হল।
উপরে বর্ণিত স্কেল অনুযায়ী A (20, 0), B (30, 12), C (40, 18), D (50, 21), E (60, 15), F (70, 6), G (80, 3) ও H (90, 0) বিন্দুগুলি স্থাপন করে এবং পরপর বিন্দুগুলিকে সরলরেখাংশ দ্বারা যুক্ত করে ABCDEFGH পরিসংখ্যা বহুভুজ অঙ্কন করা হল।

6. নীচের পরিসংখ্যা বিভাজন ছকটির পরিসংখ্যা অঙ্কন করি।

\(X\)-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের দুই বাহুকে 1 একক এবং Y অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের দুই বাহুকে 1 একক ধরা হল।
উপরের বর্ণিত স্কেল অনুযায়ী \(A (-2.5, 0)\), B (2.5, 4), C (7.5, 10), D (12.5, 24), E (17.5, 12), F (22.5, 20), G (27.5, 8) এবং H (32.5, 0) বিন্দুগুলি স্থাপন করি এবং পরপর বিন্দুগুলিকে সরলরেখাংশ দ্বারা যুক্ত করে ABCDEFGH পরিসংখ্যা বহুভুজ অঙ্কন করা হল।

7. নীচের পরিসংখ্যা বিভাজন ছকের আয়তলেখ অঙ্কন করে পরিসংখ্যা বহুভুজ অঙ্কন করি :
প্রদত্ত পরিসংখ্যা বিভাজন ছকটি শ্রেণি সাপেক্ষে নয়। এখানে দুটি ক্রমিক চাঁদার পরিমানের অন্তর 5 টাকা।
এখন, সমদৈর্ঘ্য শ্রেণি পাওয়া লক্ষ্যে 20, 25, 30, 35, ... ইত্যাদি চাঁদা সমূহকে 17.5 - 22.5; 22.5 - 27.5; 27.5 - 32.5; 32.5 – 37.5; ... ইত্যাদি শ্রেণি অন্তরের মধ্যবিন্দু নিয়ে প্রদত্ত তথ্যের আয়তলেখ ও পরিসংখ্যা বহুভুজ অঙ্কনের জন্য নিম্নলিখিত ছকটি প্রস্তুত করা হল।

\(X\)-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহু = 1 একক এবং Y-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহু = 1 একক ধরে উপরে বর্ণিত স্কেল অনুযায়ী প্রদত্ত পরিসংখ্যা বিভাজনের আয়তলেখ অঙ্কন করা হল।
আবার, একই স্কেল অনুযায়ী A (15, 0), B (20, 20), C (25, 26), D (30, 16), E (35, 10), F(40, 4), G (45, 18), H (50, 6) এবং I (55, 0) বিন্দুগুলি ছক কাগজে স্থাপন করে স্কেলের সাহায্যে পরপর বিন্দুগুলি যুক্ত করে ABCDEFGHI পরিসংখ্যা বহুভুজটি একই চিত্রে অঙ্কন করা হল।

এখন, সমদৈর্ঘ্য শ্রেণি পাওয়া লক্ষ্যে 20, 25, 30, 35, ... ইত্যাদি চাঁদা সমূহকে 17.5 - 22.5; 22.5 - 27.5; 27.5 - 32.5; 32.5 – 37.5; ... ইত্যাদি শ্রেণি অন্তরের মধ্যবিন্দু নিয়ে প্রদত্ত তথ্যের আয়তলেখ ও পরিসংখ্যা বহুভুজ অঙ্কনের জন্য নিম্নলিখিত ছকটি প্রস্তুত করা হল।

\(X\)-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহু = 1 একক এবং Y-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহু = 1 একক ধরে উপরে বর্ণিত স্কেল অনুযায়ী প্রদত্ত পরিসংখ্যা বিভাজনের আয়তলেখ অঙ্কন করা হল।
আবার, একই স্কেল অনুযায়ী A (15, 0), B (20, 20), C (25, 26), D (30, 16), E (35, 10), F(40, 4), G (45, 18), H (50, 6) এবং I (55, 0) বিন্দুগুলি ছক কাগজে স্থাপন করে স্কেলের সাহায্যে পরপর বিন্দুগুলি যুক্ত করে ABCDEFGHI পরিসংখ্যা বহুভুজটি একই চিত্রে অঙ্কন করা হল।

8. নীচের পরিসংখ্যা বিভাজন ছকের আয়তলেখ অঙ্কন করি।
প্রদত্ত পরিসংখ্যা বিভাজন ছকটি শ্রেণি সাপেক্ষে নয়। এখানে দুটি ক্রমিক শিশু সংখ্যার অন্তর 1।
এখন, সমদৈর্ঘ্য শ্রেণি পাওয়ার লক্ষ্যে নিম্নলিখিতভাবে পরিসংখ্যা বিভাজন ছক প্রস্তুত করা হল।
\(\begin{array}{|c|c|c|c|c|c|}
\hline \text { শিশু সংখ্যা } & 0-1 & 1-2 & 2-3 & 3-4 & 4-5 & 5-6\\
\hline \text { পরিবার সংখ্যা } & 120 & 85 & 50 & 25 & 15 & 5 \\
\hline
\end{array}\)
\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 5 বাহু = 1 একক এবং Y-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 1 বাহু = 1 একক ধরে প্রদত্ত পরিসংখ্যা বিভাজনের আয়তলেখ অঙ্কন করা হল।
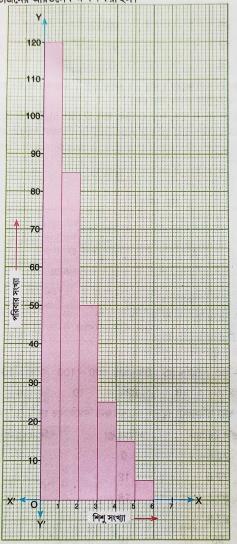
এখন, সমদৈর্ঘ্য শ্রেণি পাওয়ার লক্ষ্যে নিম্নলিখিতভাবে পরিসংখ্যা বিভাজন ছক প্রস্তুত করা হল।
\(\begin{array}{|c|c|c|c|c|c|}
\hline \text { শিশু সংখ্যা } & 0-1 & 1-2 & 2-3 & 3-4 & 4-5 & 5-6\\
\hline \text { পরিবার সংখ্যা } & 120 & 85 & 50 & 25 & 15 & 5 \\
\hline
\end{array}\)
\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 5 বাহু = 1 একক এবং Y-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 1 বাহু = 1 একক ধরে প্রদত্ত পরিসংখ্যা বিভাজনের আয়তলেখ অঙ্কন করা হল।

9. বীরসিংহ গ্রামের বিদ্যাসাগর প্রাথমিক বিদ্যালয়ে 32 জন শিক্ষক/শিক্ষিকাদের বয়সনীচের ছকে লিখলাম।

\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 1 বাহু = 1 একক এবং Y-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 3 বাহু = 1 একক ধরে প্রদত্ত তথ্য অনুযায়ী আয়তলেখ অঙ্কন করা হল।
আবার, একই স্কেল অনুযায়ী A (22, 0), B (28, 10), C (34, 13) D (40, 5), E (46, 3) F (52, 1) এবং G (58, 0) বিন্দুগুলি স্থাপন করে পরপর বিন্দুগুলি সরলরেখাংশ দ্বারা যুক্ত করে ABCDEFG পরিসংখ্যা বহুভুজ একই চিত্রে অঙ্কন করা হল।

10. নীচের পরিসংখ্যা বিভাজন ছকটির বহুভুজ অঙ্কন করি।
প্রদত্ত পরিসংখ্যা বিভাজন ছকের দ্বারা পরিসংখ্যা বহুভুজ অংশের জন্য নিম্নলিখিত ছকটি তৈরি করা হল।

\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহু = 1 একক এবং Y-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহু = 1 একক ধরে A (72.5, 0), B (77.5, 12), C (82.5, 18), D (87.5, 22), E (95, 10), F (102.5, 8) এবং G (107.5, 0) বিন্দুগুলি ছক কাগজে স্থাপন করে বিন্দুগুলিকে সরলরেখাংশ দ্বারা ক্রমান্বয়ে যুক্ত করে ABCDEFG পরিসংখ্যা বহুভুজটি অঙ্কন করা হল।


\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহু = 1 একক এবং Y-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহু = 1 একক ধরে A (72.5, 0), B (77.5, 12), C (82.5, 18), D (87.5, 22), E (95, 10), F (102.5, 8) এবং G (107.5, 0) বিন্দুগুলি ছক কাগজে স্থাপন করে বিন্দুগুলিকে সরলরেখাংশ দ্বারা ক্রমান্বয়ে যুক্ত করে ABCDEFG পরিসংখ্যা বহুভুজটি অঙ্কন করা হল।

গণিত প্রকাশ সমাধান নবম শ্রেণী || গণিত প্রকাশ রাশিবিজ্ঞান || Class 9 Chapter 11 || Ganit Prakash Class 9 Math Solution || West Bengal Board Class 9 Math || Class 9 Chapter 11 koshe dekhi 11.2 || নবম শ্রেণী কষে দেখি 11.2 || রাশিবিজ্ঞান
11. নীচের পরিসংখ্যা বিভাজন ছকটির পরিসংখ্যা বহুভুজ অঙ্কন করো :
প্রদত্ত পরিসংখ্যা বিভাজন ছকটি একটি বিচ্ছিন্ন (discontinus) পরিসংখ্যা বিভাজন ছক।
প্রথমে প্রদত্ত বিচ্ছিন্ন পরিসংখ্যা বিভাজন ছককে নিম্নলিখিতভাবে মধ্যমান সম্বলিত অবিচ্ছিন্ন পরিসংখ্যা বিভাজন ছকে পরিণত করা হল।

\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহু = 1 একক এবং Y-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 3 বাহু = 1 একক ধরে \(A (-5.5, 0)\), B (5.5, 8), C (15.5, 3), D (25.5, 6), E (35.5, 12), F (45.5, 4) এবং G (55.5, 0) বিন্দুগুলি ছক কাগজে স্থাপন করে বিন্দুগুলিকে সরলরেখাংশ দ্বারা ক্রমান্বয়ে যুক্ত করে ABCDEFG পরিসংখ্যা বহুভুজটি অঙ্কন করা হল।

প্রথমে প্রদত্ত বিচ্ছিন্ন পরিসংখ্যা বিভাজন ছককে নিম্নলিখিতভাবে মধ্যমান সম্বলিত অবিচ্ছিন্ন পরিসংখ্যা বিভাজন ছকে পরিণত করা হল।

\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহু = 1 একক এবং Y-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 3 বাহু = 1 একক ধরে \(A (-5.5, 0)\), B (5.5, 8), C (15.5, 3), D (25.5, 6), E (35.5, 12), F (45.5, 4) এবং G (55.5, 0) বিন্দুগুলি ছক কাগজে স্থাপন করে বিন্দুগুলিকে সরলরেখাংশ দ্বারা ক্রমান্বয়ে যুক্ত করে ABCDEFG পরিসংখ্যা বহুভুজটি অঙ্কন করা হল।

12. আমাদের গ্রামে সকল নারীদের স্বাক্ষর করার বিশেষ ব্যবস্থা নেওয়া হবে। তাই আমরানীচের তথ্যটি সংগ্রহ করেছি।
প্রদত্ত পরিসংখ্যা বিভাজনের পরিসংখ্যা বহুভুজ অঙ্কনের জন্য নীচের ছকটি প্রস্তুত করা হল।
\(\begin{array}{|c|c|c|c|}
\hline \text{বয়সের শ্রেণি বিভাগ} &\text{শ্রেণি মধ্যমান} & \text{স্বাক্ষরহীনের সংখ্যা (পরিসংখ্যা)} & \text{পরিসংখ্যা বহুভুজের শীর্ষবিন্দুর স্থানাঙ্ক} \\
\hline 5-10 & 7.5 & 0 & (7.5,0) \\
\hline 10-15 & 12.5 & 40 & (12.5,40) \\
\hline 15-20 & 17.5 & 90 & (17.5,90) \\
\hline 20-25 & 22.5 & 100 & (22.5,100) \\
\hline 25-30 & 27.5 & 60 & (27.5,60) \\
\hline 30-35 & 32.5 & 160 & (32.5,160) \\
\hline 35-40 & 37.5 & 0 & (37.5,0) \\
\hline
\end{array}\)
স্কেল : \(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহু = 1 একক এবং Y-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহু = 1 একক ধরে A (7.5, 0), B (12.5, 40), C (17.5, 90), D (22.5, 100), E (27.5, 60), F (32.5, 160) ও G (37.5, 0) বিন্দুগুলি ছক কাগজে স্থাপন করে বিন্দুগুলিকে সরলরেখাংশ দ্বারা ক্রমান্বয়ে যুক্ত করে ABCDEFG পরিসংখ্যা বহুভুজটি অঙ্কন করা হল।

\(\begin{array}{|c|c|c|c|}
\hline \text{বয়সের শ্রেণি বিভাগ} &\text{শ্রেণি মধ্যমান} & \text{স্বাক্ষরহীনের সংখ্যা (পরিসংখ্যা)} & \text{পরিসংখ্যা বহুভুজের শীর্ষবিন্দুর স্থানাঙ্ক} \\
\hline 5-10 & 7.5 & 0 & (7.5,0) \\
\hline 10-15 & 12.5 & 40 & (12.5,40) \\
\hline 15-20 & 17.5 & 90 & (17.5,90) \\
\hline 20-25 & 22.5 & 100 & (22.5,100) \\
\hline 25-30 & 27.5 & 60 & (27.5,60) \\
\hline 30-35 & 32.5 & 160 & (32.5,160) \\
\hline 35-40 & 37.5 & 0 & (37.5,0) \\
\hline
\end{array}\)
স্কেল : \(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহু = 1 একক এবং Y-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহু = 1 একক ধরে A (7.5, 0), B (12.5, 40), C (17.5, 90), D (22.5, 100), E (27.5, 60), F (32.5, 160) ও G (37.5, 0) বিন্দুগুলি ছক কাগজে স্থাপন করে বিন্দুগুলিকে সরলরেখাংশ দ্বারা ক্রমান্বয়ে যুক্ত করে ABCDEFG পরিসংখ্যা বহুভুজটি অঙ্কন করা হল।

13. গত মাসে কলকাতা ফুটবল-লিগে দলগুলির দেওয়া গোলের পরিসংখ্যা দেওয়া হল।
প্রদত্ত তথ্যের পরিসংখ্যা বহুভুজ অঙ্কনের জন্য নীচের ছকটি তৈরি করা হল।
\(\begin{array}{|c|c|c|c|}
\hline \text{স্কোর} & \text{পরিসংখ্যা} & \text{পরিসংখ্যা বহুভুজের শীর্ষবিন্দুর স্থানাঙ্ক}\\
\hline-1 & 0 & (-1,0) \\
\hline 0 & 15 & (0,15) \\
\hline 1 & 20 & (1,20) \\
\hline 2 & 12 & (2,12) \\
\hline 3 & 8 & (3,8) \\
\hline 4 & 6 & (4,6) \\
\hline 5 & 3 & (5,3) \\
\hline 6 & 1 & (6,1) \\
\hline 7 & 0 & (7,0) \\
\hline
\end{array}\)

\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 5 বাহু = 1 একক এবং Y-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 5 বাহু = 1 একক ধরে \(A (-1, 0)\), B (0, 15), C (1, 20), D (2, 12), E (3, 8), F (4, 6), G (5, 3), H (6, 1) এবং I (7, 0) বিন্দুগুলি ছক কাগজে স্থাপন করে বিন্দুগুলিকে পরপর সরলরেখাংশ দ্বারা যুক্ত করে ABCDEFGHI পরিসংখ্যা বহুভুজটি অঙ্কন করা হল।
\(\begin{array}{|c|c|c|c|}
\hline \text{স্কোর} & \text{পরিসংখ্যা} & \text{পরিসংখ্যা বহুভুজের শীর্ষবিন্দুর স্থানাঙ্ক}\\
\hline-1 & 0 & (-1,0) \\
\hline 0 & 15 & (0,15) \\
\hline 1 & 20 & (1,20) \\
\hline 2 & 12 & (2,12) \\
\hline 3 & 8 & (3,8) \\
\hline 4 & 6 & (4,6) \\
\hline 5 & 3 & (5,3) \\
\hline 6 & 1 & (6,1) \\
\hline 7 & 0 & (7,0) \\
\hline
\end{array}\)

\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 5 বাহু = 1 একক এবং Y-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 5 বাহু = 1 একক ধরে \(A (-1, 0)\), B (0, 15), C (1, 20), D (2, 12), E (3, 8), F (4, 6), G (5, 3), H (6, 1) এবং I (7, 0) বিন্দুগুলি ছক কাগজে স্থাপন করে বিন্দুগুলিকে পরপর সরলরেখাংশ দ্বারা যুক্ত করে ABCDEFGHI পরিসংখ্যা বহুভুজটি অঙ্কন করা হল।
14. বহু বিকল্পীয় প্রশ্নাবলি (M.C.Q.) :
(i) একটি আয়তলেখর প্রতিটি আয়তক্ষেত্রের ক্ষেত্রফল সমানুপাতী হবে
(a) ওই শ্রেণির মধ্যবিন্দুর সাথে (b) ওই শ্রেণির শ্রেণি দৈর্ঘ্যের সাথে
(c) ওই শ্রেণির পরিসংখ্যার সাথে (d) ওই শ্রেণির ক্রমযৌগিক পরিসংখ্যার সাথে
(a) ওই শ্রেণির মধ্যবিন্দুর সাথে (b) ওই শ্রেণির শ্রেণি দৈর্ঘ্যের সাথে
(c) ওই শ্রেণির পরিসংখ্যার সাথে (d) ওই শ্রেণির ক্রমযৌগিক পরিসংখ্যার সাথে
একটি আয়তলেখর প্রতিটি আয়তক্ষেত্রের ক্ষেত্রফল সমানুপাতী হবে ওই শ্রেণির পরিসংখ্যার সঙ্গে।
(ii) একটি পরিসংখ্যা বহুভূজ অঙ্কন করা হয় শ্রেণির পরিসংখ্যা এবং
(a) শ্রেণির উচ্চ সীমানা দ্বারা (b) শ্রেণির নিম্ন সীমানা দ্বারা
(c) শ্রেণির মধ্যমান দ্বারা (d) শ্রেণির যেকোনো মান দ্বারা
(a) শ্রেণির উচ্চ সীমানা দ্বারা (b) শ্রেণির নিম্ন সীমানা দ্বারা
(c) শ্রেণির মধ্যমান দ্বারা (d) শ্রেণির যেকোনো মান দ্বারা
একটি পরিসংখ্যা বহুভুজ অঙ্কন করা হয় শ্রেণির পরিসংখ্যা এবং শ্রেণির মধ্যমান দ্বারা।
(iii) আয়তলেখ অঙ্কনের ক্ষেত্রে শ্রেণি সীমানা নেওয়া যায়।
(a) y-অক্ষ বরাবর (b) \(x\)-অক্ষ বরাবর
(c) \(x\)-অক্ষ এবং y-অক্ষ উভয় বরাবর (d) \(x\)-অক্ষ ও y-অক্ষের মধ্যে
(a) y-অক্ষ বরাবর (b) \(x\)-অক্ষ বরাবর
(c) \(x\)-অক্ষ এবং y-অক্ষ উভয় বরাবর (d) \(x\)-অক্ষ ও y-অক্ষের মধ্যে
আয়তলেখ অঙ্কনের ক্ষেত্রে শ্রেণি সীমানা নেওয়া হয় অক্ষ বরাবর।
(iv) আয়তলেখ অঙ্কনের ক্ষেত্রে প্রতিটি আয়তক্ষেত্রের ভুমি হয়।
(a) পরিসীমা (b) শ্রেণিসীমানা (c) প্রসার (d) শ্রেণি দৈর্ঘ্য
(a) পরিসীমা (b) শ্রেণিসীমানা (c) প্রসার (d) শ্রেণি দৈর্ঘ্য
আয়তলেখ অঙ্কনের ক্ষেত্রে প্রতিটি শ্রেণির আয়তক্ষেত্রের ভূমি হয় শ্রেণি দৈর্ঘ্য।
(v) একটি আয়তলেখ বিন্যস্ত তথ্যের লৈখিক প্রকাশ যার শ্রেণি-সীমানা ও পরিসংখ্যানেওয়া হয় যথাক্রমে
(a) উল্লম্ব ও অনুভূমিক অক্ষ বরাবর (b) কেবলমাত্র উল্লম্ব অক্ষ বরাবর
(c) কেবলমাত্র অনুভূমিক অক্ষ বরাবর (d) অনুভূমিক ও উল্লম্ব অক্ষ বরাবর
(a) উল্লম্ব ও অনুভূমিক অক্ষ বরাবর (b) কেবলমাত্র উল্লম্ব অক্ষ বরাবর
(c) কেবলমাত্র অনুভূমিক অক্ষ বরাবর (d) অনুভূমিক ও উল্লম্ব অক্ষ বরাবর
একটি আয়তলেখ বিন্যস্ত তথ্যের লৈখিক প্রকাশ যার শ্রেণি-সীমা এবং পরিসংখ্যা নেওয়া হয় যথাক্রমে অনুভূমিক ও উল্লম্ব অক্ষ বরাবর।
গণিত প্রকাশ সমাধান নবম শ্রেণী || গণিত প্রকাশ রাশিবিজ্ঞান || Class 9 Chapter 11 || Ganit Prakash Class 9 Math Solution || West Bengal Board Class 9 Math || Class 9 Chapter 11 koshe dekhi 11.2 || নবম শ্রেণী কষে দেখি 11.2 || রাশিবিজ্ঞান
এই Page টি বা এই Website টির কোন প্রকার বিষয়বস্তু কপি করা বা সম্পাদনা করা নিষিদ্ধ। ভারতীয় Copywright আইন 1957 এর ধারা 63 অনুযায়ী, এই ফাইলটির সমস্ত অধিকার 'ছাত্র মিত্র Mathematics' অ্যাপ দ্বারা সংরক্ষিত। ছাত্র মিত্রের অনুমতি ছাড়া, এই Page টি বা এই Website টির কোন প্রকার বিষয়বস্তু কপি করা বা সম্পাদনা করা আইনত দন্ডনীয় অপরাধ। কেউ ছাত্র মিত্রের অনুমতি ছাড়া, এই Page টি বা এই Website টির কোন প্রকার বিষয়বস্তু কপি বা সম্পাদনা করলে ছাত্র মিত্র কতৃপক্ষ তার বিরুদ্ধে সকল প্রকার কঠোর আইনি পদক্ষেপ করবে।
West Bengal Board of Secondary Education Official Site
Class 8 : গণিত প্রভা (অষ্টম শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali.
Class 7 : গণিত প্রভা (সপ্তম শ্রেণি) বইয়ের সমস্ত সমাধান
www.wbresults.nic.in Official
Class 10 : মাধ্যমিক গণিত প্রকাশ (দশম শ্রেণি) বইয়ের সমস্ত সমাধান Class 10 Maths Solution WBBSE Bengali
Class 6 : গণিত প্রভা (ষষ্ঠ শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali
Class 9 : গণিত প্রকাশ (নবম শ্রেণি) বইয়ের সমাধান Maths Solution WBBSE Bengali
আজই Install করুন Chatra Mitra
Class 8 : গণিত প্রভা (অষ্টম শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali.
Class 7 : গণিত প্রভা (সপ্তম শ্রেণি) বইয়ের সমস্ত সমাধান
www.wbresults.nic.in Official
Class 10 : মাধ্যমিক গণিত প্রকাশ (দশম শ্রেণি) বইয়ের সমস্ত সমাধান Class 10 Maths Solution WBBSE Bengali
Class 6 : গণিত প্রভা (ষষ্ঠ শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali
Class 9 : গণিত প্রকাশ (নবম শ্রেণি) বইয়ের সমাধান Maths Solution WBBSE Bengali
আজই Install করুন Chatra Mitra
গণিত প্রকাশ সমাধান নবম শ্রেণী || গণিত প্রকাশ রাশিবিজ্ঞান || Class 9 Chapter 11 || Ganit Prakash Class 9 Math Solution || West Bengal Board Class 9 Math || Class 9 Chapter 11 koshe dekhi 11.2 || নবম শ্রেণী কষে দেখি 11.2 || রাশিবিজ্ঞান
কষে দেখি - 11.2
গণিত প্রকাশ সমাধান নবম শ্রেণী || গণিত প্রকাশ রাশিবিজ্ঞান || Class 9 Chapter 11 || Ganit Prakash Class 9 Math Solution || West Bengal Board Class 9 Math || Class 9 Chapter 11 koshe dekhi 11.2 || নবম শ্রেণী কষে দেখি 11.2 || রাশিবিজ্ঞান
1. বকুলতলা গ্রামের 50টি দোকানের দৈনিক লাভ (টাকায়) নীচের ছক করে লিখলাম-
\(\begin{array}{|c|c|c|c|c|c|}
\hline \text { দৈনিক লাভ (Rs.) } & 0-50 & 50-100 & 100-150 & 150-200 & 200-250 \\
\hline \text { দোকানের সংখ্যা } & 8 & 15 & 10 & 12 & 5 \\
\hline
\end{array}\)
\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 1 বাহুকে 5 একক এবং Y অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহুকে 1 একক ধরে প্রদত্ত তথ্যের আয়তলেখ করা হল।

\hline \text { দৈনিক লাভ (Rs.) } & 0-50 & 50-100 & 100-150 & 150-200 & 200-250 \\
\hline \text { দোকানের সংখ্যা } & 8 & 15 & 10 & 12 & 5 \\
\hline
\end{array}\)
\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 1 বাহুকে 5 একক এবং Y অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহুকে 1 একক ধরে প্রদত্ত তথ্যের আয়তলেখ করা হল।

2. মিতা তাদের স্কুলের 75 জন বন্ধুদের উচ্চতা মেপে নীচের ছকে লিখল।
\(\begin{array}{|c|c|c|c|c|c|}
\hline \text { উচ্চতা (সেমি) } & 136-142 & 142-148 & 148-154 & 154-160 & 160-166 \\
\hline \text { বন্ধুদের সংখ্যা } & 12 & 18 & 26 & 14 & 05 \\
\hline
\end{array}\)
\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহুকে 1 একক এবং Y অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহুকে 1 একক ধরা হল। মিতার সংগৃহীত তথ্যের আয়তলেখটি নিম্নরূপ :

\hline \text { উচ্চতা (সেমি) } & 136-142 & 142-148 & 148-154 & 154-160 & 160-166 \\
\hline \text { বন্ধুদের সংখ্যা } & 12 & 18 & 26 & 14 & 05 \\
\hline
\end{array}\)
\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহুকে 1 একক এবং Y অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহুকে 1 একক ধরা হল। মিতার সংগৃহীত তথ্যের আয়তলেখটি নিম্নরূপ :

3. আমাদের পাড়ার 10 বছর থেকে বছর 45 বয়স পর্যন্ত বাসিন্দাদের মধ্যে হিন্দিভাষীলোকের সংখ্যা সংগ্রহ করে নীচের ছকে লিখলাম।
প্রদত্ত পরিসংখ্যা বিভাজন ছকটি বিচ্ছিন্ন (discontinuous) পরিসংখ্যা বিভাজন ছক। প্রথমে প্রদত্ত বিচ্ছিন্ন পরিসংখ্যা বিভাজন ছককে নিম্নে অবিচ্ছিন্ন পরিসংখ্যা বিভাজন ছকে পরিণত করা হল।
\(\begin{array}{|c|c|c|c|c|c|c|}
\hline \text { শ্রেণি বিভাগ } & 9.5-15.5 & 15.5-21.5 & 21.5-27.5 & 27.5-33.5 & 33.5-39.5 & 39.5-45.5\\
\hline \text { পরিসংখ্যা } & 8 & 14 & 10 & 20 & 6 & 12 \\
\hline
\end{array}\)
\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহুকে 1 একক এবং Y অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহুকে 1 একক ধরে প্রদত্ত তথ্যের আয়তলেখ অঙ্কিত হল।

\(\begin{array}{|c|c|c|c|c|c|c|}
\hline \text { শ্রেণি বিভাগ } & 9.5-15.5 & 15.5-21.5 & 21.5-27.5 & 27.5-33.5 & 33.5-39.5 & 39.5-45.5\\
\hline \text { পরিসংখ্যা } & 8 & 14 & 10 & 20 & 6 & 12 \\
\hline
\end{array}\)
\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহুকে 1 একক এবং Y অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহুকে 1 একক ধরে প্রদত্ত তথ্যের আয়তলেখ অঙ্কিত হল।

4. নীচের পরিসংখ্যা বিভাজন ছকটির আয়তলেখ অঙ্কন করি :
প্রদত্ত পরিসংখ্যা বিভাজন ছকটি বিচ্ছিন্ন (discontinuous) পরিসংখ্যা বিভাজন ছক। প্রথমে প্রদত্ত বিচ্ছিন্ন পরিসংখ্যা বিভাজন ছককে নিম্নে অবিচ্ছিন্ন পরিসংখ্যা বিভাজন ছকে পরিণত করা হল।
\(\begin{array}{|c|c|c|c|c|c|c|}
\hline \text { শ্রেণি } & 0.5-10.5 & 10.5-20.5 & 20.5-30.5 & 30.5-40.5 & 40.5-50.5 & 50.5-60.5\\
\hline \text { পরিসংখ্যা } & 8 & 3 & 6 & 12 & 2 & 7 \\
\hline
\end{array}\)
\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহুকে = 1 একক এবং Y-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহুকে = 1 একক ধরে প্রদত্ত তথ্যের আয়তলেখ অঙ্কিত হল।

\(\begin{array}{|c|c|c|c|c|c|c|}
\hline \text { শ্রেণি } & 0.5-10.5 & 10.5-20.5 & 20.5-30.5 & 30.5-40.5 & 40.5-50.5 & 50.5-60.5\\
\hline \text { পরিসংখ্যা } & 8 & 3 & 6 & 12 & 2 & 7 \\
\hline
\end{array}\)
\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহুকে = 1 একক এবং Y-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহুকে = 1 একক ধরে প্রদত্ত তথ্যের আয়তলেখ অঙ্কিত হল।

গণিত প্রকাশ সমাধান নবম শ্রেণী || গণিত প্রকাশ রাশিবিজ্ঞান || Class 9 Chapter 11 || Ganit Prakash Class 9 Math Solution || West Bengal Board Class 9 Math || Class 9 Chapter 11 koshe dekhi 11.2 || নবম শ্রেণী কষে দেখি 11.2 || রাশিবিজ্ঞান
5. পৃথাদের স্কুলের 75 জন শিক্ষার্থীদের নিম্নলিখিত প্রাপ্ত নম্বরের পরিসংখ্যা বহুভুজ অঙ্কন করি।
প্রদত্ত পরিসংখ্যা বিভাজনের পরিসংখ্যা বহুভুজ অঙ্কনের জন্য প্রথমে নীচের ছক প্রস্তুত করা হল।

(i) \(X\)-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের একবাহু = 1 একক এবং
(ii) Y-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের পাঁচ বাহুর দৈর্ঘ্য = 1 একক ধরা হল।
উপরে বর্ণিত স্কেল অনুযায়ী A (20, 0), B (30, 12), C (40, 18), D (50, 21), E (60, 15), F (70, 6), G (80, 3) ও H (90, 0) বিন্দুগুলি স্থাপন করে এবং পরপর বিন্দুগুলিকে সরলরেখাংশ দ্বারা যুক্ত করে ABCDEFGH পরিসংখ্যা বহুভুজ অঙ্কন করা হল।


(i) \(X\)-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের একবাহু = 1 একক এবং
(ii) Y-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের পাঁচ বাহুর দৈর্ঘ্য = 1 একক ধরা হল।
উপরে বর্ণিত স্কেল অনুযায়ী A (20, 0), B (30, 12), C (40, 18), D (50, 21), E (60, 15), F (70, 6), G (80, 3) ও H (90, 0) বিন্দুগুলি স্থাপন করে এবং পরপর বিন্দুগুলিকে সরলরেখাংশ দ্বারা যুক্ত করে ABCDEFGH পরিসংখ্যা বহুভুজ অঙ্কন করা হল।

6. নীচের পরিসংখ্যা বিভাজন ছকটির পরিসংখ্যা অঙ্কন করি।

\(X\)-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের দুই বাহুকে 1 একক এবং Y অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের দুই বাহুকে 1 একক ধরা হল।
উপরের বর্ণিত স্কেল অনুযায়ী \(A (-2.5, 0)\), B (2.5, 4), C (7.5, 10), D (12.5, 24), E (17.5, 12), F (22.5, 20), G (27.5, 8) এবং H (32.5, 0) বিন্দুগুলি স্থাপন করি এবং পরপর বিন্দুগুলিকে সরলরেখাংশ দ্বারা যুক্ত করে ABCDEFGH পরিসংখ্যা বহুভুজ অঙ্কন করা হল।

7. নীচের পরিসংখ্যা বিভাজন ছকের আয়তলেখ অঙ্কন করে পরিসংখ্যা বহুভুজ অঙ্কন করি :
প্রদত্ত পরিসংখ্যা বিভাজন ছকটি শ্রেণি সাপেক্ষে নয়। এখানে দুটি ক্রমিক চাঁদার পরিমানের অন্তর 5 টাকা।
এখন, সমদৈর্ঘ্য শ্রেণি পাওয়া লক্ষ্যে 20, 25, 30, 35, ... ইত্যাদি চাঁদা সমূহকে 17.5 - 22.5; 22.5 - 27.5; 27.5 - 32.5; 32.5 – 37.5; ... ইত্যাদি শ্রেণি অন্তরের মধ্যবিন্দু নিয়ে প্রদত্ত তথ্যের আয়তলেখ ও পরিসংখ্যা বহুভুজ অঙ্কনের জন্য নিম্নলিখিত ছকটি প্রস্তুত করা হল।

\(X\)-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহু = 1 একক এবং Y-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহু = 1 একক ধরে উপরে বর্ণিত স্কেল অনুযায়ী প্রদত্ত পরিসংখ্যা বিভাজনের আয়তলেখ অঙ্কন করা হল।
আবার, একই স্কেল অনুযায়ী A (15, 0), B (20, 20), C (25, 26), D (30, 16), E (35, 10), F(40, 4), G (45, 18), H (50, 6) এবং I (55, 0) বিন্দুগুলি ছক কাগজে স্থাপন করে স্কেলের সাহায্যে পরপর বিন্দুগুলি যুক্ত করে ABCDEFGHI পরিসংখ্যা বহুভুজটি একই চিত্রে অঙ্কন করা হল।

এখন, সমদৈর্ঘ্য শ্রেণি পাওয়া লক্ষ্যে 20, 25, 30, 35, ... ইত্যাদি চাঁদা সমূহকে 17.5 - 22.5; 22.5 - 27.5; 27.5 - 32.5; 32.5 – 37.5; ... ইত্যাদি শ্রেণি অন্তরের মধ্যবিন্দু নিয়ে প্রদত্ত তথ্যের আয়তলেখ ও পরিসংখ্যা বহুভুজ অঙ্কনের জন্য নিম্নলিখিত ছকটি প্রস্তুত করা হল।

\(X\)-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহু = 1 একক এবং Y-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহু = 1 একক ধরে উপরে বর্ণিত স্কেল অনুযায়ী প্রদত্ত পরিসংখ্যা বিভাজনের আয়তলেখ অঙ্কন করা হল।
আবার, একই স্কেল অনুযায়ী A (15, 0), B (20, 20), C (25, 26), D (30, 16), E (35, 10), F(40, 4), G (45, 18), H (50, 6) এবং I (55, 0) বিন্দুগুলি ছক কাগজে স্থাপন করে স্কেলের সাহায্যে পরপর বিন্দুগুলি যুক্ত করে ABCDEFGHI পরিসংখ্যা বহুভুজটি একই চিত্রে অঙ্কন করা হল।

8. নীচের পরিসংখ্যা বিভাজন ছকের আয়তলেখ অঙ্কন করি।
প্রদত্ত পরিসংখ্যা বিভাজন ছকটি শ্রেণি সাপেক্ষে নয়। এখানে দুটি ক্রমিক শিশু সংখ্যার অন্তর 1।
এখন, সমদৈর্ঘ্য শ্রেণি পাওয়ার লক্ষ্যে নিম্নলিখিতভাবে পরিসংখ্যা বিভাজন ছক প্রস্তুত করা হল।
\(\begin{array}{|c|c|c|c|c|c|}
\hline \text { শিশু সংখ্যা } & 0-1 & 1-2 & 2-3 & 3-4 & 4-5 & 5-6\\
\hline \text { পরিবার সংখ্যা } & 120 & 85 & 50 & 25 & 15 & 5 \\
\hline
\end{array}\)
\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 5 বাহু = 1 একক এবং Y-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 1 বাহু = 1 একক ধরে প্রদত্ত পরিসংখ্যা বিভাজনের আয়তলেখ অঙ্কন করা হল।

এখন, সমদৈর্ঘ্য শ্রেণি পাওয়ার লক্ষ্যে নিম্নলিখিতভাবে পরিসংখ্যা বিভাজন ছক প্রস্তুত করা হল।
\(\begin{array}{|c|c|c|c|c|c|}
\hline \text { শিশু সংখ্যা } & 0-1 & 1-2 & 2-3 & 3-4 & 4-5 & 5-6\\
\hline \text { পরিবার সংখ্যা } & 120 & 85 & 50 & 25 & 15 & 5 \\
\hline
\end{array}\)
\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 5 বাহু = 1 একক এবং Y-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 1 বাহু = 1 একক ধরে প্রদত্ত পরিসংখ্যা বিভাজনের আয়তলেখ অঙ্কন করা হল।

9. বীরসিংহ গ্রামের বিদ্যাসাগর প্রাথমিক বিদ্যালয়ে 32 জন শিক্ষক/শিক্ষিকাদের বয়সনীচের ছকে লিখলাম।

\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 1 বাহু = 1 একক এবং Y-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 3 বাহু = 1 একক ধরে প্রদত্ত তথ্য অনুযায়ী আয়তলেখ অঙ্কন করা হল।
আবার, একই স্কেল অনুযায়ী A (22, 0), B (28, 10), C (34, 13) D (40, 5), E (46, 3) F (52, 1) এবং G (58, 0) বিন্দুগুলি স্থাপন করে পরপর বিন্দুগুলি সরলরেখাংশ দ্বারা যুক্ত করে ABCDEFG পরিসংখ্যা বহুভুজ একই চিত্রে অঙ্কন করা হল।

10. নীচের পরিসংখ্যা বিভাজন ছকটির বহুভুজ অঙ্কন করি।
প্রদত্ত পরিসংখ্যা বিভাজন ছকের দ্বারা পরিসংখ্যা বহুভুজ অংশের জন্য নিম্নলিখিত ছকটি তৈরি করা হল।

\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহু = 1 একক এবং Y-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহু = 1 একক ধরে A (72.5, 0), B (77.5, 12), C (82.5, 18), D (87.5, 22), E (95, 10), F (102.5, 8) এবং G (107.5, 0) বিন্দুগুলি ছক কাগজে স্থাপন করে বিন্দুগুলিকে সরলরেখাংশ দ্বারা ক্রমান্বয়ে যুক্ত করে ABCDEFG পরিসংখ্যা বহুভুজটি অঙ্কন করা হল।


\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহু = 1 একক এবং Y-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহু = 1 একক ধরে A (72.5, 0), B (77.5, 12), C (82.5, 18), D (87.5, 22), E (95, 10), F (102.5, 8) এবং G (107.5, 0) বিন্দুগুলি ছক কাগজে স্থাপন করে বিন্দুগুলিকে সরলরেখাংশ দ্বারা ক্রমান্বয়ে যুক্ত করে ABCDEFG পরিসংখ্যা বহুভুজটি অঙ্কন করা হল।

গণিত প্রকাশ সমাধান নবম শ্রেণী || গণিত প্রকাশ রাশিবিজ্ঞান || Class 9 Chapter 11 || Ganit Prakash Class 9 Math Solution || West Bengal Board Class 9 Math || Class 9 Chapter 11 koshe dekhi 11.2 || নবম শ্রেণী কষে দেখি 11.2 || রাশিবিজ্ঞান
11. নীচের পরিসংখ্যা বিভাজন ছকটির পরিসংখ্যা বহুভুজ অঙ্কন করো :
প্রদত্ত পরিসংখ্যা বিভাজন ছকটি একটি বিচ্ছিন্ন (discontinus) পরিসংখ্যা বিভাজন ছক।
প্রথমে প্রদত্ত বিচ্ছিন্ন পরিসংখ্যা বিভাজন ছককে নিম্নলিখিতভাবে মধ্যমান সম্বলিত অবিচ্ছিন্ন পরিসংখ্যা বিভাজন ছকে পরিণত করা হল।

\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহু = 1 একক এবং Y-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 3 বাহু = 1 একক ধরে \(A (-5.5, 0)\), B (5.5, 8), C (15.5, 3), D (25.5, 6), E (35.5, 12), F (45.5, 4) এবং G (55.5, 0) বিন্দুগুলি ছক কাগজে স্থাপন করে বিন্দুগুলিকে সরলরেখাংশ দ্বারা ক্রমান্বয়ে যুক্ত করে ABCDEFG পরিসংখ্যা বহুভুজটি অঙ্কন করা হল।

প্রথমে প্রদত্ত বিচ্ছিন্ন পরিসংখ্যা বিভাজন ছককে নিম্নলিখিতভাবে মধ্যমান সম্বলিত অবিচ্ছিন্ন পরিসংখ্যা বিভাজন ছকে পরিণত করা হল।

\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহু = 1 একক এবং Y-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 3 বাহু = 1 একক ধরে \(A (-5.5, 0)\), B (5.5, 8), C (15.5, 3), D (25.5, 6), E (35.5, 12), F (45.5, 4) এবং G (55.5, 0) বিন্দুগুলি ছক কাগজে স্থাপন করে বিন্দুগুলিকে সরলরেখাংশ দ্বারা ক্রমান্বয়ে যুক্ত করে ABCDEFG পরিসংখ্যা বহুভুজটি অঙ্কন করা হল।

12. আমাদের গ্রামে সকল নারীদের স্বাক্ষর করার বিশেষ ব্যবস্থা নেওয়া হবে। তাই আমরানীচের তথ্যটি সংগ্রহ করেছি।
প্রদত্ত পরিসংখ্যা বিভাজনের পরিসংখ্যা বহুভুজ অঙ্কনের জন্য নীচের ছকটি প্রস্তুত করা হল।
\(\begin{array}{|c|c|c|c|}
\hline \text{বয়সের শ্রেণি বিভাগ} &\text{শ্রেণি মধ্যমান} & \text{স্বাক্ষরহীনের সংখ্যা (পরিসংখ্যা)} & \text{পরিসংখ্যা বহুভুজের শীর্ষবিন্দুর স্থানাঙ্ক} \\
\hline 5-10 & 7.5 & 0 & (7.5,0) \\
\hline 10-15 & 12.5 & 40 & (12.5,40) \\
\hline 15-20 & 17.5 & 90 & (17.5,90) \\
\hline 20-25 & 22.5 & 100 & (22.5,100) \\
\hline 25-30 & 27.5 & 60 & (27.5,60) \\
\hline 30-35 & 32.5 & 160 & (32.5,160) \\
\hline 35-40 & 37.5 & 0 & (37.5,0) \\
\hline
\end{array}\)
স্কেল : \(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহু = 1 একক এবং Y-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহু = 1 একক ধরে A (7.5, 0), B (12.5, 40), C (17.5, 90), D (22.5, 100), E (27.5, 60), F (32.5, 160) ও G (37.5, 0) বিন্দুগুলি ছক কাগজে স্থাপন করে বিন্দুগুলিকে সরলরেখাংশ দ্বারা ক্রমান্বয়ে যুক্ত করে ABCDEFG পরিসংখ্যা বহুভুজটি অঙ্কন করা হল।

\(\begin{array}{|c|c|c|c|}
\hline \text{বয়সের শ্রেণি বিভাগ} &\text{শ্রেণি মধ্যমান} & \text{স্বাক্ষরহীনের সংখ্যা (পরিসংখ্যা)} & \text{পরিসংখ্যা বহুভুজের শীর্ষবিন্দুর স্থানাঙ্ক} \\
\hline 5-10 & 7.5 & 0 & (7.5,0) \\
\hline 10-15 & 12.5 & 40 & (12.5,40) \\
\hline 15-20 & 17.5 & 90 & (17.5,90) \\
\hline 20-25 & 22.5 & 100 & (22.5,100) \\
\hline 25-30 & 27.5 & 60 & (27.5,60) \\
\hline 30-35 & 32.5 & 160 & (32.5,160) \\
\hline 35-40 & 37.5 & 0 & (37.5,0) \\
\hline
\end{array}\)
স্কেল : \(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহু = 1 একক এবং Y-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 2 বাহু = 1 একক ধরে A (7.5, 0), B (12.5, 40), C (17.5, 90), D (22.5, 100), E (27.5, 60), F (32.5, 160) ও G (37.5, 0) বিন্দুগুলি ছক কাগজে স্থাপন করে বিন্দুগুলিকে সরলরেখাংশ দ্বারা ক্রমান্বয়ে যুক্ত করে ABCDEFG পরিসংখ্যা বহুভুজটি অঙ্কন করা হল।

13. গত মাসে কলকাতা ফুটবল-লিগে দলগুলির দেওয়া গোলের পরিসংখ্যা দেওয়া হল।
প্রদত্ত তথ্যের পরিসংখ্যা বহুভুজ অঙ্কনের জন্য নীচের ছকটি তৈরি করা হল।
\(\begin{array}{|c|c|c|c|}
\hline \text{স্কোর} & \text{পরিসংখ্যা} & \text{পরিসংখ্যা বহুভুজের শীর্ষবিন্দুর স্থানাঙ্ক}\\
\hline-1 & 0 & (-1,0) \\
\hline 0 & 15 & (0,15) \\
\hline 1 & 20 & (1,20) \\
\hline 2 & 12 & (2,12) \\
\hline 3 & 8 & (3,8) \\
\hline 4 & 6 & (4,6) \\
\hline 5 & 3 & (5,3) \\
\hline 6 & 1 & (6,1) \\
\hline 7 & 0 & (7,0) \\
\hline
\end{array}\)

\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 5 বাহু = 1 একক এবং Y-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 5 বাহু = 1 একক ধরে \(A (-1, 0)\), B (0, 15), C (1, 20), D (2, 12), E (3, 8), F (4, 6), G (5, 3), H (6, 1) এবং I (7, 0) বিন্দুগুলি ছক কাগজে স্থাপন করে বিন্দুগুলিকে পরপর সরলরেখাংশ দ্বারা যুক্ত করে ABCDEFGHI পরিসংখ্যা বহুভুজটি অঙ্কন করা হল।
\(\begin{array}{|c|c|c|c|}
\hline \text{স্কোর} & \text{পরিসংখ্যা} & \text{পরিসংখ্যা বহুভুজের শীর্ষবিন্দুর স্থানাঙ্ক}\\
\hline-1 & 0 & (-1,0) \\
\hline 0 & 15 & (0,15) \\
\hline 1 & 20 & (1,20) \\
\hline 2 & 12 & (2,12) \\
\hline 3 & 8 & (3,8) \\
\hline 4 & 6 & (4,6) \\
\hline 5 & 3 & (5,3) \\
\hline 6 & 1 & (6,1) \\
\hline 7 & 0 & (7,0) \\
\hline
\end{array}\)

\(X\)-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 5 বাহু = 1 একক এবং Y-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 5 বাহু = 1 একক ধরে \(A (-1, 0)\), B (0, 15), C (1, 20), D (2, 12), E (3, 8), F (4, 6), G (5, 3), H (6, 1) এবং I (7, 0) বিন্দুগুলি ছক কাগজে স্থাপন করে বিন্দুগুলিকে পরপর সরলরেখাংশ দ্বারা যুক্ত করে ABCDEFGHI পরিসংখ্যা বহুভুজটি অঙ্কন করা হল।
14. বহু বিকল্পীয় প্রশ্নাবলি (M.C.Q.) :
(i) একটি আয়তলেখর প্রতিটি আয়তক্ষেত্রের ক্ষেত্রফল সমানুপাতী হবে
(a) ওই শ্রেণির মধ্যবিন্দুর সাথে (b) ওই শ্রেণির শ্রেণি দৈর্ঘ্যের সাথে
(c) ওই শ্রেণির পরিসংখ্যার সাথে (d) ওই শ্রেণির ক্রমযৌগিক পরিসংখ্যার সাথে
(a) ওই শ্রেণির মধ্যবিন্দুর সাথে (b) ওই শ্রেণির শ্রেণি দৈর্ঘ্যের সাথে
(c) ওই শ্রেণির পরিসংখ্যার সাথে (d) ওই শ্রেণির ক্রমযৌগিক পরিসংখ্যার সাথে
একটি আয়তলেখর প্রতিটি আয়তক্ষেত্রের ক্ষেত্রফল সমানুপাতী হবে ওই শ্রেণির পরিসংখ্যার সঙ্গে।
(ii) একটি পরিসংখ্যা বহুভূজ অঙ্কন করা হয় শ্রেণির পরিসংখ্যা এবং
(a) শ্রেণির উচ্চ সীমানা দ্বারা (b) শ্রেণির নিম্ন সীমানা দ্বারা
(c) শ্রেণির মধ্যমান দ্বারা (d) শ্রেণির যেকোনো মান দ্বারা
(a) শ্রেণির উচ্চ সীমানা দ্বারা (b) শ্রেণির নিম্ন সীমানা দ্বারা
(c) শ্রেণির মধ্যমান দ্বারা (d) শ্রেণির যেকোনো মান দ্বারা
একটি পরিসংখ্যা বহুভুজ অঙ্কন করা হয় শ্রেণির পরিসংখ্যা এবং শ্রেণির মধ্যমান দ্বারা।
(iii) আয়তলেখ অঙ্কনের ক্ষেত্রে শ্রেণি সীমানা নেওয়া যায়।
(a) y-অক্ষ বরাবর (b) \(x\)-অক্ষ বরাবর
(c) \(x\)-অক্ষ এবং y-অক্ষ উভয় বরাবর (d) \(x\)-অক্ষ ও y-অক্ষের মধ্যে
(a) y-অক্ষ বরাবর (b) \(x\)-অক্ষ বরাবর
(c) \(x\)-অক্ষ এবং y-অক্ষ উভয় বরাবর (d) \(x\)-অক্ষ ও y-অক্ষের মধ্যে
আয়তলেখ অঙ্কনের ক্ষেত্রে শ্রেণি সীমানা নেওয়া হয় অক্ষ বরাবর।
(iv) আয়তলেখ অঙ্কনের ক্ষেত্রে প্রতিটি আয়তক্ষেত্রের ভুমি হয়।
(a) পরিসীমা (b) শ্রেণিসীমানা (c) প্রসার (d) শ্রেণি দৈর্ঘ্য
(a) পরিসীমা (b) শ্রেণিসীমানা (c) প্রসার (d) শ্রেণি দৈর্ঘ্য
আয়তলেখ অঙ্কনের ক্ষেত্রে প্রতিটি শ্রেণির আয়তক্ষেত্রের ভূমি হয় শ্রেণি দৈর্ঘ্য।
(v) একটি আয়তলেখ বিন্যস্ত তথ্যের লৈখিক প্রকাশ যার শ্রেণি-সীমানা ও পরিসংখ্যানেওয়া হয় যথাক্রমে
(a) উল্লম্ব ও অনুভূমিক অক্ষ বরাবর (b) কেবলমাত্র উল্লম্ব অক্ষ বরাবর
(c) কেবলমাত্র অনুভূমিক অক্ষ বরাবর (d) অনুভূমিক ও উল্লম্ব অক্ষ বরাবর
(a) উল্লম্ব ও অনুভূমিক অক্ষ বরাবর (b) কেবলমাত্র উল্লম্ব অক্ষ বরাবর
(c) কেবলমাত্র অনুভূমিক অক্ষ বরাবর (d) অনুভূমিক ও উল্লম্ব অক্ষ বরাবর
একটি আয়তলেখ বিন্যস্ত তথ্যের লৈখিক প্রকাশ যার শ্রেণি-সীমা এবং পরিসংখ্যা নেওয়া হয় যথাক্রমে অনুভূমিক ও উল্লম্ব অক্ষ বরাবর।
গণিত প্রকাশ সমাধান নবম শ্রেণী || গণিত প্রকাশ রাশিবিজ্ঞান || Class 9 Chapter 11 || Ganit Prakash Class 9 Math Solution || West Bengal Board Class 9 Math || Class 9 Chapter 11 koshe dekhi 11.2 || নবম শ্রেণী কষে দেখি 11.2 || রাশিবিজ্ঞান
এই Page টি বা এই Website টির কোন প্রকার বিষয়বস্তু কপি করা বা সম্পাদনা করা নিষিদ্ধ। ভারতীয় Copywright আইন 1957 এর ধারা 63 অনুযায়ী, এই ফাইলটির সমস্ত অধিকার 'ছাত্র মিত্র Mathematics' অ্যাপ দ্বারা সংরক্ষিত। ছাত্র মিত্রের অনুমতি ছাড়া, এই Page টি বা এই Website টির কোন প্রকার বিষয়বস্তু কপি করা বা সম্পাদনা করা আইনত দন্ডনীয় অপরাধ। কেউ ছাত্র মিত্রের অনুমতি ছাড়া, এই Page টি বা এই Website টির কোন প্রকার বিষয়বস্তু কপি বা সম্পাদনা করলে ছাত্র মিত্র কতৃপক্ষ তার বিরুদ্ধে সকল প্রকার কঠোর আইনি পদক্ষেপ করবে।
West Bengal Board of Secondary Education Official Site
Class 8 : গণিত প্রভা (অষ্টম শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali.
Class 7 : গণিত প্রভা (সপ্তম শ্রেণি) বইয়ের সমস্ত সমাধান
www.wbresults.nic.in Official
Class 10 : মাধ্যমিক গণিত প্রকাশ (দশম শ্রেণি) বইয়ের সমস্ত সমাধান Class 10 Maths Solution WBBSE Bengali
Class 6 : গণিত প্রভা (ষষ্ঠ শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali
Class 9 : গণিত প্রকাশ (নবম শ্রেণি) বইয়ের সমাধান Maths Solution WBBSE Bengali
আজই Install করুন Chatra Mitra
Class 8 : গণিত প্রভা (অষ্টম শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali.
Class 7 : গণিত প্রভা (সপ্তম শ্রেণি) বইয়ের সমস্ত সমাধান
www.wbresults.nic.in Official
Class 10 : মাধ্যমিক গণিত প্রকাশ (দশম শ্রেণি) বইয়ের সমস্ত সমাধান Class 10 Maths Solution WBBSE Bengali
Class 6 : গণিত প্রভা (ষষ্ঠ শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali
Class 9 : গণিত প্রকাশ (নবম শ্রেণি) বইয়ের সমাধান Maths Solution WBBSE Bengali
আজই Install করুন Chatra Mitra



