WBBSE Class 9 Math koshe dekhi 12 || West Bengal Board Class 9 Math Solution Chapter 12 || Class 9 Solution koshe dekhi 12 || ক্ষেত্রফল সংক্রান্ত উপপাদ্য || Ganit Prakash Class 9 Solution koshe dekhi 12 || Ganit Prakash Solution Class 9 In Bengali || গণিত প্রকাশ সমাধান নবম শ্রেণী || গণিত প্রকাশ ক্ষেত্রফল সংক্রান্ত উপপাদ্য (Class-9) কষে দেখি 12 || West Bengal Board Class 9 Math Solution Chapter 12 ক্ষেত্রফল সংক্রান্ত উপপাদ্য
Share this page using :
নবম শ্রেণী কষে দেখি 12 || ক্ষেত্রফল সংক্রান্ত উপপাদ্য || Class 9 Chapter 12 || Ganit Prakash Class 9 Math Solution || West Bengal Board Class 9 Math || Class 9 Chapter 12 koshe dekhi 12
কষে দেখি - 12
নবম শ্রেণী কষে দেখি 12 || ক্ষেত্রফল সংক্রান্ত উপপাদ্য || Class 9 Chapter 12 || Ganit Prakash Class 9 Math Solution || West Bengal Board Class 9 Math || Class 9 Chapter 12 koshe dekhi 12
1. ABCD সামান্তরিকের AB এবং DC বাহর মধ্যবিন্দ যথাক্রমে P এবং Q; প্রমাণ করি যে, APCQ চতুর্ভুজাকার ক্ষেত্রের ক্ষেত্রফল = \(\frac{1}{2} \times A B C D\) সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল।

প্রদত্ত : ABCD সামান্তরিকের AB ও DC বাহুর মধ্যবিন্দু যথাক্রমে P ও Q।
AQ ও CP অঙ্কন করা হল।
প্রামাণ্য বিষয় : APCQ চতুর্ভুজাকার ক্ষেত্রের ক্ষেত্রফল \(=\frac{1}{2} \times \mathrm{ABCD}\) সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল।
অঙ্কন : A, C যুক্ত করা হল।
প্রমাণ : যেহেতু, ABCD সামান্তরিক।
\(\therefore\) AB = CD এবং \({A B} \| C D\)
\(\therefore \frac{1}{2} A B=\frac{1}{2} C D \)
\(\therefore A P=C Q\)
\(\therefore\) APCQ-র AP = CQ এবং \(\mathrm{AP} \| \mathrm{CQ}\)
\(\therefore\) APCQ একটি সামান্তরিক।
APCQ সামান্তরিকের কর্ণ AC হওয়ায়
\(\triangle \mathrm{APC}=\triangle \mathrm{AQC}=x\) (মনে করি)
\(\because \triangle \mathrm{ABC}\)-র CP মধ্যমা, \(\triangle \mathrm{ABC}\)-কে দুটি সমান ক্ষেত্রফলবিশিষ্ট ত্রিভুজে বিভক্ত করে,
\(\therefore \triangle \mathrm{BPC}=\triangle \mathrm{APC}=x\)
আবার, \(\triangle \mathrm{ADC}\)-র AQ মধ্যমা হওয়ায়
\(\triangle \mathrm{ADQ}=\triangle \mathrm{AQC}=x\)
\(\therefore\) ABCD সামান্তরিকের ক্ষেত্রফল
\(=(\triangle \mathrm{ADQ}+\triangle \mathrm{AQC}+\triangle \mathrm{APC}+\triangle \mathrm{BPC})\)-র ক্ষেত্রফল
\(=(x+x+x+x)=4 x\)
\(\therefore\) APCQ-র ক্ষেত্রফল \(=(\triangle \mathrm{APC}+\triangle \mathrm{AQC})\)-র ক্ষেত্রফল
\(=(x+x)=2 x=\frac{1}{2} \times 4 x\)
\(=\frac{1}{2} \times A B C D\) সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল (প্রমাণিত)
2. ABCD রম্বসের AB ও DC বাহুর মধ্যে দূরত্ব PQ এবং AD ও BC বাহর মধ্যে দূরত্ব RS; প্রমাণ করি যে, \(PQ = RS\)

প্রদত্ত : ABCD রম্বসের AB ও DC-র মধ্যে লম্বদূরত্ব PQ এবং AD ও BC-র মধ্যে লম্বদূরত্ব RS।
প্রামাণ্য বিষয় : PQ = RS
প্রমাণ : যেহেতু, AB-কে ভূমি ও PQ-কে উচ্চতা ধরলে ABCD রম্বসের
ক্ষেত্রফল = ভূমি \( \times \) উচ্চতা \(=A B \times P Q\ldots(i)\)
আবার, AD-কে ভূমি ও RS-কে উচ্চতা ধরলে,
ABCD রম্বসের ক্ষেত্রফল \(=A D \times R S\ldots(ii)\)
(i) ও (ii) হতে পাই,
\(A B \times P Q=A D \times R S\)
বা, \(A B \times P Q=A B \times R S\)
\(\quad\quad\) [\(\because\) ABCD একটি রম্বস যার সকল বাহুর দৈর্ঘ্য সমান]
বা, PQ = RS (প্রমাণিত)
3. ABCD সামান্তরিকের AB এবং DC বাহুর মধ্য বিন্দু যথাক্রমে P ও Q; প্রমাণ করি যে, PBQD একটি সামান্তরিক এবং \(\Delta P B C=\frac{1}{2}\) সামান্তরিক PBQD.

প্রদত্ত : ABCD সামান্তরিকের AB ও CD-র মধ্যবিন্দু যথাক্রমে P ও Q।
P, D ও B, Q এবং P, C যুক্ত করা হল।
প্রামাণ্য বিষয় : (i) PBQD একটি সামান্তরিক।
(ii) \(\triangle \mathrm{PBC}=\frac{1}{2} \times\) সামান্তরিক PBQD।
প্রমাণ : যেহেতু, ABCD একটি সামান্তরিক,
\(\therefore\) AB = DC এবং \(A B \| D C\)
\(\therefore \frac{1}{2} A B=\frac{1}{2} D C\quad\) [উভয়পক্ষে \(\frac{1}{2}\) গুণ করে পাই]
\(\therefore\) PB = DQ
\(\therefore\) PBQD চতুর্ভুজের PB = DQ এবং \(P B \| D Q\)
\(\therefore\) PBQD একটি সামান্তরিক। [(i) প্রমাণিত ]
\(\because \triangle \mathrm{PBC}\) ও সামান্তরিক PBQD একই ভূমি PB ও একই সমান্তরালযুগল PB ও CD-র মধ্যে অবস্থিত।
\(\therefore \triangle \mathrm{PBC}=\frac{1}{2} \times\) সামান্তরিক PBQD [(ii) প্রমাণিত]
4. ABC সমদ্বিবাহু ত্রিভুজের \(AB = AC\) এবং বর্ধিত BC বাহুর উপর P যেকোনো একটি বিন্দু। P বিন্দু থেকে AB এবং AC বাহুর উপর যথাক্রমে PQ ও PR লম্ব। B বিন্দু থেকে AC বাহুর লম্ব BS; প্রমাণ করি যে, \(PQ – PR = BS\)

প্রদত্ত : \(\triangle \mathrm{ABC}\)-র AB = AC এবং বর্ধিত BC-র উপর P একটি বিন্দু।
P হতে AB ও AC (বর্ধিত)-র উপর PQ ও PR লম্ব।
B হতে AC-র উপর BS লম্ব।
প্রামাণ্য বিষয় : \(PQ - PR = BS\)
অঙ্কন : A, P যুক্ত করা হল।
প্রমাণ : \(\triangle \mathrm{ABP}=\triangle \mathrm{ABC}+\triangle \mathrm{ACP}\)
বা, \(\frac{1}{2} \times A B \times P Q=\frac{1}{2} \times A C \times B S+\frac{1}{2} \times A C \times P R \)
বা, \(A B \times P Q=A B \times B S+A B \times P R\quad[\because A B=A C]\)
বা, \(P Q=B S+P R\)
বা, \(P Q-P R=B S\) (প্রমাণিত)
5. ABC সমবাহু ত্রিভুজের বাইরে এবং ABC কৌণিক অঞ্চলের মধ্যে O যেকোনো একটি বিন্দু। O বিন্দু থেকে AB, BC এবং CA বাহুর উপর লম্ব যথাক্রমে OP, OQ এবং OR; প্রমাণ করি যে, ত্রিভুজটির উচ্চতা \(= OP + OQ - OR\)

প্রদত্ত : ABC একটি সমবাহু ত্রিভুজ যার AB = BC = CA।
ABC কৌণিক অঞ্চলে O যে-কোনো একটি বিন্দু।
O হতে AB, বর্ধিত BC ও CA-র উপর যথাক্রমে OP, OQ ও OR লম্ব।
প্রামাণ্য বিষয় : \(\triangle A B C\)-র উচ্চতা \(= OP + OQ - OR\)
অঙ্কন : শীর্ষবিন্দু A হতে BC-র উপর AM লম্ব অঙ্কন করা হল।
A, O; B, O ও C, O যুক্ত করা হল।
প্রমাণ : \(\triangle \mathrm{ABC}=\triangle \mathrm{ABO}+\triangle \mathrm{BCO}-\triangle \mathrm{ACO}\)
বা, \(\frac{1}{2} \times B C \times A M =\frac{1}{2} \times A B \times O P+\frac{1}{2} \times B C \times O Q-\frac{1}{2} \times A C \times O R \)
বা, \(B C \times A M=A B \times O P+B C \times O Q-A C \times O R \)
বা, \(B C \times A M=B C \times O P+B C \times O Q-B C \times O R\quad[\because A B=B C=C A]\)
বা, \(A M=O P+O Q-O R\)
\(\therefore \triangle \mathrm{ABC}\)-র উচ্চতা \(=O P+O Q-O R\) (প্রমাণিত)
6. ABCD সামান্তরিকের AB বাহুর সমান্তরাল সরলরেখা AD, AC এবং BC কে বা তাদের বর্ধিত অংশকে যথাক্রমে E, F ও G বিন্দুতে ছেদ করে। প্রমাণ করি যে, \(\Delta A E G=A F D\).

প্রদত্ত : ABCD সামান্তরিকের AB বাহুর সমান্তরাল সরলরেখা AD, AC এবং BC কে যথাক্রমে E, F ও G বিন্দুতে ছেদ করেছে।
প্রামাণ্য বিষয় : \(\triangle \mathrm{AEG}=\triangle \mathrm{AFD}\)
অঙ্কন : F বিন্দু দিয়ে BC বাহুর সমান্তরাল সরলরেখা অঙ্কন করা হল যা AB ও CD কে যথাক্রমে P ও Q বিন্দুতে ছেদ করে।
প্রমাণ : প্রদত্ত চিত্রে, \(E G\|A B\| D C\) এবং \(P Q\|B C\| A D\)
\(\therefore\) APFE এবং FGCQ দুটি সামান্তরিক যাদের কর্ণদ্বয় যথাক্রমে AF ও FC
\(\therefore \triangle \mathrm{APF}=\triangle \mathrm{AEF}\ldots(i)\)
এবং \(\Delta \mathrm{FGC}=\Delta \mathrm{FCQ}\ldots(ii)\)
[\(\because\) সামান্তরিকের কর্ণ উহাকে দুটি সমান ক্ষেত্রফলবিশিষ্ট ত্রিভুজে বিভক্ত করে]
আবার, \(\because\) ABCD সামান্তরিকের AC কর্ণ,
\(\therefore \triangle \mathrm{ABC}=\triangle \mathrm{ADC}\)
বা, \(\triangle \mathrm{APF}+\) সামান্তরিক \(\mathrm{PBGF}+\Delta \mathrm{FGC} =\triangle \mathrm{AEF}+\) সামান্তরিক \(EFQD + \triangle \mathrm{FQC}\)
বা, \(\triangle A P F+\) সামান্তরিক \(\mathrm{PBGF}+\Delta \mathrm{FGC}=\Delta \mathrm{APF}+\) সামান্তরিক
\(\mathrm{EFQD}+\Delta \mathrm{FGC}\quad\) [(i) ও (ii) হতে পাই]
বা, সামান্তরিক PBGF = সামান্তরিক EFQD
বা, সামান্তরিক PBGF + সামান্তরিক APFE = সামান্তরিক EFQD + সামান্তরিক APFE [উভয়পক্ষে সামান্তরিক APFE যুক্ত করে পাই]
বা, সামান্তরিক ABGE = সামান্তরিক APQD \(\ldots(iii)\)
এখন, যেহেতু, সামান্তরিক ABGE-র AG কর্ণ
\(\therefore \triangle A E G=\frac{1}{2} \times\) সামান্তরিক ABGE \(ABGE \ldots(iv)\)
[\(\because\) সামান্তরিকের কর্ণ উহাকে সমান ক্ষেত্রফলবিশিষ্ট দুটি ত্রিভুজে বিভক্ত করে]
আবার, \(\because \triangle A F D\) ও সামান্তরিক APQD একই ভূমি AD ও একই সমান্তরালযুগল AD ও PQ-র মধ্যে অবস্থিত।
\(\therefore \triangle \mathrm{AFD}=\frac{1}{2} \times\) সামান্তরিক\( APQD\)
\(=\frac{1}{2} \times\) সামান্তরিক \(ABGE\quad\) [(iii) হতে পাই]
\(=\triangle \mathrm{AEG}\quad\) [(iv) হতে পাই]
\(\therefore \triangle \mathrm{AEG}=\triangle \mathrm{AFD}\) (প্রমাণিত)
নবম শ্রেণী কষে দেখি 12 || ক্ষেত্রফল সংক্রান্ত উপপাদ্য || Class 9 Chapter 12 || Ganit Prakash Class 9 Math Solution || West Bengal Board Class 9 Math || Class 9 Chapter 12 koshe dekhi 12
7. ABCD সামান্তরিকের DC বাহুর উপর E যে-কোনো একটি বিন্দু। বর্ধিত AE, বর্ধিত BC-কে F বিন্দুতে ছেদ করে। D, F যুক্ত করা হল। প্রমাণ করি যে, (i) \(\Delta A D F=\Delta A B E\) (ii) \(\Delta D E F=\Delta B E C\)

প্রদত্ত : ABCD সামান্তরিকের DC বাহুর উপর E যে-কোনো একটি বিন্দু। বর্ধিত AE, বর্ধিত BC-কে F বিন্দুতে ছেদ করে। D, F যুক্ত করা হল।
প্রামাণ্য বিষয় : (i) \(\triangle \mathrm{ADF}=\triangle \mathrm{ABE}\) ও (ii) \(\triangle \mathrm{DEF}=\triangle \mathrm{BEC}\)
প্রমাণ : যেহেতু, \(\triangle \mathrm{ADF}\) ও সামান্তরিক ABCD একই ভূমি AD ও একই সমান্তরালযুগল AD ও BF-র মধ্যে অবস্থিত,
\(\therefore \triangle \mathrm{ADF}=\frac{1}{2} \times\) সমান্তরিক \(ABCD \ldots (1)\)
আবার, \(\because \triangle \mathrm{ABE}\) ও সামান্তরিক ABCD একই ভূমি AB ও একই সমান্তরাল যুগল AB ও DC-র মধ্যে অবস্থিত।
\(\therefore \triangle \mathrm{ABE}=\frac{1}{2} \times\) সামান্তরিক \(ABCD \ldots(2)\)
\(\therefore\) (1) ও (2) হতে পাই, \(\triangle \mathrm{ADF}=\triangle \mathrm{ABE}\quad\) [প্রমাণিত (i) নং]
যেহেতু, \(\triangle \mathrm{ABE}=\frac{1}{2} \times\) সামান্তরিক ABCD
\(\therefore 2 \triangle \mathrm{ABE}=\) সামান্তরিক \(ABCD\)
বা, \(2 \triangle \mathrm{ABE}=\triangle \mathrm{ABE}+\triangle \mathrm{ADE}+\triangle \mathrm{BEC} \)
বা, \(\triangle \mathrm{ABE}=\triangle \mathrm{ADE}+\triangle \mathrm{BEC}\)
\(\therefore \frac{1}{2} \times \) সামান্তরিক \(\mathrm{ABCD}=\triangle \mathrm{ADE}+\triangle \mathrm{BEC}\)
বা, \(\triangle \mathrm{ADF}=\triangle \mathrm{ADE}+\triangle \mathrm{BEC}\quad\) [(1) থেকে পাই]
বা, \(\triangle \mathrm{ADE}+\triangle \mathrm{DEF}=\Delta \mathrm{ADE}+\triangle \mathrm{BEC}\)
\(\therefore \triangle D E F=\triangle B E C\quad\) [প্রমানিত (ii) নং]
8. সমান ক্ষেত্রফল বিশিষ্ট ABC এবং ABD দুটি ত্রিভুজাকার ক্ষেত্র AB বাহুর বিপরীত দিকে অবস্থিত। প্রমাণ করি যে, AB, CD-কে সমদ্বিখণ্ডিত করে।

প্রদত্ত : সমান ক্ষেত্রফলবিশিষ্ট \(\triangle \mathrm{ABC}\) ও \(\triangle \mathrm{ABD}\) একই ভূমি AB-র পরস্পর বিপরীত পার্শ্বে অবস্থিত। C, D যুক্ত করা হল। AB ও CD পরস্পরকে O বিন্দুতে ছেদ করে।
প্রামাণ্য বিষয় : AB, CD কে সমদ্বিখণ্ডিত করে অর্থাৎ CO = DO।
অঙ্কন : C ও D বিন্দু হতে AB-র উপর যথাক্রমে CP ও DQ লম্ব অঙ্কন করা হল।P, D ও C, Q যুক্ত করা হল।
প্রমাণ : যেহেতু, \(\triangle \mathrm{ABC}=\triangle \mathrm{ABD}\) [প্রদত্ত]
\(\therefore \frac{1}{2} \times \mathrm{AB} \times \mathrm{CP}=\frac{1}{2} \times \mathrm{AB} \times \mathrm{DQ} \)
\( \therefore \mathrm{CP}=\mathrm{DQ}\)
আবার, একই বাহু AB-র উপর CP ও DQ লম্ব হওয়ায় \(\mathrm{CP} \| \mathrm{DQ}\)
এখন, CPDQ চতুর্ভুজের CP = DQ এবং \(\mathrm{CP} \| \mathrm{DQ}\)
\(\therefore\) CPDQ একটি সামান্তরিক। আমরা জানি, সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে।
\(\therefore\) PQ এবং CD কর্ণদ্বয় পরস্পরকে O বিন্দুতে সমদ্বিখণ্ডিত করে।
\(\therefore\) O বিন্দু CD-র মধ্যবিন্দু।
\(\therefore\) AB, CD কে সমদ্বিখণ্ডিত করে অর্থাৎ CO = DO (প্রমাণিত)
9. ABC ত্রিভুজের BC বাহুর মধ্যে বিন্দু D; CDEF সামান্তরিকটি BC বাহু এবং A বিন্দু দিয়ে BC বাহুর সমান্তরাল সরলরেখার মধ্যে অবস্থিত। প্রমাণ করি যে, \(\Delta A B C\) = সামান্তরিক \(CDEF\)

প্রদত্ত : \(\triangle \mathrm{ABC}\)-র BC বাহুর মধ্যবিন্দু D। CDEF সামান্তরিকটি BC বাহু ও A বিন্দু দিয়ে BC বাহুর সমান্তরাল সরলরেখার মধ্যে অবস্থিত।
প্রামাণ্য বিষয় : \(\triangle \mathrm{ABC}\) = সামান্তরিক CDEF
অঙ্কন : A, D যুক্ত করা হল।
প্রমাণ : সামান্তরিক CDEF ও \(\triangle \mathrm{ADC}\) একই ভূমি CD এবং একই সমান্তরালযুগলের মধ্যে অবস্থিত।
\(\therefore \triangle \mathrm{ACD}=\frac{1}{2} \times\) সামান্তরিক CDEF
অর্থাৎ, \(2 \times \triangle \mathrm{ACD}=\) সামান্তরিক \(CDEF \ldots(i)\)
আবার, \(\triangle \mathrm{ABC}\)-র AD মধ্যমা হওয়ায়
\(\triangle \mathrm{ABC}=2 \times \triangle \mathrm{ACD}\ldots(ii)\)
[\(\because\) ত্রিভুজের মধ্যমা ত্রিভুজকে দুটি সমান ক্ষেত্রফলবিশিষ্ট ত্রিভুজে বিভক্ত করে]
(i) ও (ii) হতে পাই, \(\triangle \mathrm{ABC}\) = সামান্তরিক CDEF (প্রমাণিত)
10. ABCD সামান্তরিকের BD কর্ণের উপর P যেকোনো একটি বিন্দু। প্রমাণ করো যে, \(\Delta A P D=\Delta C P D\).

প্রদত্ত : ABCD সামান্তরিকের BD কর্ণের উপর P একটি বিন্দু।
প্রামাণ্য বিষয় : \(\triangle \mathrm{APD}=\triangle \mathrm{CPD}\)
অঙ্কন : A ও C বিন্দু দিয়ে BD-র উপর যথাক্রমে AM ও CN লম্ব অঙ্কন করা হল।
প্রমাণ : যেহেতু, ABCD সামান্তরিকের BD কর্ণ,
\(\therefore \triangle \mathrm{ABD}=\triangle \mathrm{DBC}\)
বা, \(\frac{1}{2} \times B D \times A M=\frac{1}{2} \times B D \times C N\)
\(\therefore \mathrm{AM}=\mathrm{CN}\)
এখন, \(\triangle \mathrm{APD}=\frac{1}{2} \times \mathrm{PD} \times \mathrm{AM}\)
\(=\frac{1}{2} \times \mathrm{PD} \times \mathrm{CN}\quad[\because \mathrm{AM}=\mathrm{CN}]\)
\(=\triangle C P D\) (প্রমাণিত)
11. ABC ত্রিভুজের AD ও BE মধ্যমা। প্রমাণ করি যে, \(\Delta A C D=\Delta B C E\)

প্রদত্ত : \(\triangle \mathrm{ABC}\)-র AD ও BE মধ্যমা।
প্রামাণ্য বিষয় : \(\triangle \mathrm{ACD}=\triangle \mathrm{BCE}\)
প্রমাণ : যেহেতু, কোনো ত্রিভুজের একটি মধ্যমা ত্রিভুজটিকে দুটি সমান ক্ষেত্রফলবিশিষ্ট ত্রিভুজে বিভক্ত করে।
\(\therefore \triangle \mathrm{ACD}=\Delta \mathrm{ABD}=\frac{1}{2} \Delta \mathrm{ABC}\ldots(i)\)
আবার, \(\triangle \mathrm{BCE}=\Delta \mathrm{BEA}=\frac{1}{2} \Delta \mathrm{ABC}\ldots (ii)\)
\(\therefore\) (i) ও (ii) হতে পাই, \(\triangle \mathrm{ACD}=\Delta \mathrm{BCE}\) (প্রমাণিত)
12. ABC ত্রিভুজের BC বাহুর সমান্তরাল সরলরেখা AB এবং AC বাহুকে যথাক্রমে P ও Q বিন্দুতে ছেদ করে। CP এবং BQ পরস্পরকে \(X\) বিন্দুতে ছেদ করে। প্রমাণ করি যে, (i) \(\Delta B P Q=\Delta C P Q\) (ii) \(\Delta B C P=\Delta B C Q\) (iii) \(\Delta A C P=\Delta A B Q\) (iv) \(\Delta B X P=\Delta C X Q\)

প্রদত্ত : \(\triangle \mathrm{ABC}\)-র BC বাহুর সমান্তরাল সরলরেখা AB ও AC বাহুকে যথাক্রমে P ও Q বিন্দুতে ছেদ করে। CP ও BQ পরস্পরকে \(X\) বিন্দুতে ছেদ করে।
প্রামাণ্য বিষয় : (i) \(\triangle \mathrm{BPQ}=\triangle \mathrm{CPQ}\)
(ii) \(\triangle \mathrm{BCP}=\triangle \mathrm{BCQ}\)
(iii) \(\triangle \mathrm{ACP}=\triangle \mathrm{ABQ}\)
(iv) \(\triangle \mathrm{BXP}=\triangle \mathrm{CXQ}\)
প্রমাণ : যেহেতু, \(B C \| P Q\) এবং \(\triangle \mathrm{BPQ}\) ও \(\triangle \mathrm{CPQ}\) একই ভূমি PQ ও একই সমান্তরালযুগল PQ ও BC-র মধ্যে অবস্থিত।
\(\therefore \triangle \mathrm{BPQ}=\triangle \mathrm{CPQ}\) [\(\because\) একই ভূমি ও একই সমান্তরালযুগলের মধ্যে অবস্থিত দুটি ত্রিভুজের ক্ষেত্রফল সমান।] [(i) প্রমাণিত]
আবার, \(\triangle \mathrm{BCP}\) ও \(\triangle \mathrm{BCQ}\) একই ভূমি BC ও একই সমান্তরাল যুগল BC ও PQ-র মধ্যে অবস্থিত।
\(\therefore \triangle B C P=\triangle B C Q\) [\(\because\) একই ভূমি ও একই সমান্তরালযুগলের মধ্যে অবস্থিত দুটি ত্রিভুজের ক্ষেত্রফল সমান] [(ii) প্রমাণিত]
\(\because \triangle \mathrm{BPQ}=\triangle \mathrm{CPQ}\quad\) [(i) নং হতে পাই]
বা, \(\Delta \mathrm{BPQ}+\Delta \mathrm{APQ}=\Delta \mathrm{CPQ}+\Delta \mathrm{APQ}\quad\) [উভয়পক্ষে \(\triangle \mathrm{APQ}\) যোগ করে পাই]
বা, \(\triangle \mathrm{ABQ}=\triangle \mathrm{ACP}\)
\(\therefore \triangle \mathrm{ACP}=\triangle \mathrm{ABQ}\quad\) [(iii) প্রমাণিত]
আবার, \( \triangle \mathrm{BPQ}=\Delta \mathrm{CPQ}\quad \) [(i) হতে পাই]
\(\therefore \triangle \mathrm{BXP}+\Delta \mathrm{PQX}=\Delta \mathrm{CXQ}+\Delta \mathrm{PQX}\)
\(\therefore \triangle B X P=\triangle C X Q\quad\) [(iv) প্রমাণিত]
13. ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D এবং BC বাহুর উপর P যেকোন একটি বিন্দু। P, A যুক্ত করি। D বিন্দু দিয়ে PA সরলরেখাংশ সমান্তরাল সরলরেখা AB বাহুকে Q বিন্দুতে ছেদ করে। প্রমাণ করি যে, (i) \(\Delta A D Q=\Delta P D Q\) (ii) \(\Delta B P Q=\frac{1}{2} \Delta A B C\)

প্রদত্ত : \(\triangle A B C\)-র BC বাহুর মধ্যবিন্দু D এবং BC বাহুর উপর P একটি বিন্দু। P, A যুক্ত করা হল। D বিন্দু দিয়ে PA-র সমান্তরাল সরলরেখা AB কে Q বিন্দুতে ছেদ করে।
প্রমাণ্য বিষয় : (i) \(\triangle \mathrm{ADQ}=\triangle \mathrm{PDQ}\) এবং
(ii) \(\triangle \mathrm{BPQ}=\frac{1}{2} \Delta \mathrm{ABC}\)
প্রমাণ : \(\triangle \mathrm{ADQ}\) ও \(\triangle \mathrm{PDQ}\) একই ভূমি DQ ও একই সমান্তরাল যুগল \(\mathrm{DQ} \| \mathrm{AP}\)-র মধ্যে অবস্থিত।
\(\therefore \triangle \mathrm{ADQ}=\triangle \mathrm{PDQ}\) [\(\because\) একই ভূমি ও একই সমান্তরালযুগলের মধ্যে অবস্থিত সকল ত্রিভুজের ক্ষেত্রফল সমান] [(i) নং প্রমাণিত]
আবার, \(\because \triangle \mathrm{ADQ}=\triangle \mathrm{PDQ}\)
বা, \(\Delta \mathrm{BDQ}+\Delta \mathrm{ADQ}=\Delta \mathrm{BDQ}+\Delta \mathrm{PDQ}\)
\(\therefore \triangle \mathrm{ABD}=\triangle \mathrm{BPQ}\)
বা, \(\frac{1}{2} \triangle \mathrm{ABC}=\Delta \mathrm{BPQ}\)
\(\left[\right.\because \triangle \mathrm{ABC}\)-র AD মধ্যমা এবং মধ্যমা ত্রিভুজকে দুটি সমান ক্ষেত্রফলবিশিষ্ট ত্রিভুজে বিভক্ত করে অর্থাৎ
\(\left.\triangle \mathrm{ABD}=\triangle \mathrm{ADC}=\frac{1}{2} \triangle \mathrm{ABC}\right]\)
\(\therefore \triangle \mathrm{BPQ}=\frac{1}{2} \Delta \mathrm{ABC}\quad\) [(ii) নং প্রমাণিত]
14. ABC ত্রিভুজে AB = AC; B ও C বিন্দু থেকে AB ও AC বাহুর উপর লম্ব যথাক্রমে AC ও AB বাহুকে E ও F বিন্দুতে ছেদ করে। প্রমাণ করি যে, \(\mathbf{F E} \| \mathbf{B C}\)
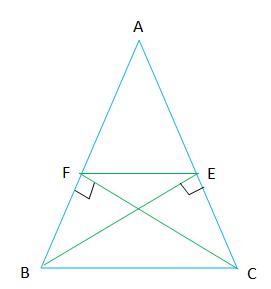
প্রদত্ত : \(\triangle \mathrm{ABC}\)-র AB = AC। B ও C বিন্দু থেকে AC ও AB-র উপর অঙ্কিত লম্বদ্বয় যথাক্রমে BE ও CF।
প্রামাণ্য বিষয় : \(F E \| B C\)
প্রমাণ : \(\triangle \mathrm{ABC}=\frac{1}{2} \times \mathrm{AB} \times \mathrm{CF}\ldots(i)\)
আবার, \(\triangle \mathrm{ABC}=\frac{1}{2} \times \mathrm{AC} \times \mathrm{BE}\ldots(ii)\)
(i) ও (ii) হতে পাই, \(\frac{1}{2} \times A B \times C F=\frac{1}{2} \times A C \times B E\)
বা, \(\frac{1}{2} \times \mathrm{AB} \times \mathrm{CF}=\frac{1}{2} \times \mathrm{AB} \times \mathrm{BE}\quad[\because \mathrm{AB}=\mathrm{AC}]\)
\(\therefore C F=B E\)
\(\triangle B E C\) ও \(\triangle \mathrm{BFC}\)-র
(i) BE = CF (পূর্বে প্রমাণিত)
(ii) \(\angle \mathrm{BEC}=\angle \mathrm{BFC}\) [স্বীকার] এবং
(iii) BC সাধারণ বাহু
\(\therefore \triangle B E C \cong \triangle B F C\quad \) [R-H-S শর্তে]
\(\therefore \triangle B E C=\triangle B F C\)
এখন, \(\triangle B E C\) ও \(\triangle \mathrm{BFC}\) একই ভূমি BC-র উপর অবস্থিত এবং এদের ক্ষেত্রফল সমান হওয়ায় ত্রিভুজদ্বয় একই সমান্তরালযুগলের মধ্যে অবস্থিত হবে।
\(\therefore B C \| E F\) (প্রমাণিত)
নবম শ্রেণী কষে দেখি 12 || ক্ষেত্রফল সংক্রান্ত উপপাদ্য || Class 9 Chapter 12 || Ganit Prakash Class 9 Math Solution || West Bengal Board Class 9 Math || Class 9 Chapter 12 koshe dekhi 12
15. ABC ত্রিভুজে \(\angle A B C=\angle A C B ;\angle \mathrm{ABC}\) ও \( \angle \mathrm{ACB}\)কোণের সমদ্বিখণ্ডকদ্বয় AC ও AB বাহুকে যথাক্রমে E ও F বিন্দুতে ছেদ করে। প্রমাণ করি যে, \(F E \| B C\)

প্রদত্ত : \(\triangle \mathrm{ABC}\)-র \(\angle \mathrm{ABC}=\angle \mathrm{ACB} ; \angle \mathrm{ABC}\) ও \(\angle \mathrm{ACB}\)-র সমদ্বিখণ্ডকদ্বয় AC ও AB বাহুকে যথাক্রমে E ও F বিন্দুতে ছেদ করে।
প্রামাণ্য বিষয় : \(\mathrm{FE} \| \mathrm{BC}\)
প্রমাণ : \(\triangle \mathrm{BFC}\) ও \(\triangle \mathrm{BEC}\)-র
(i) \(\angle \mathrm{FBC}=\angle \mathrm{ECB}\quad[\because \angle \mathrm{ABC}=\angle \mathrm{ACB}]\)
(ii) \(\angle \mathrm{FCB}=\angle \mathrm{EBC}\quad\left[\because \frac{1}{2} \angle \mathrm{ABC}(=\angle \mathrm{EBC})=\frac{1}{2} \angle \mathrm{ACB}(=\mathrm{ECB})\right] \)
(iii) BC সাধারণ বাহু
আবার, \(\triangle \mathrm{BFC} \cong \triangle \mathrm{BEC}\quad\) [A-S-A শর্তে]
\(\therefore \triangle B F C=\triangle B E C\)
\(\triangle \mathrm{BFC}\) ও \(\triangle \mathrm{BEC}\) একই ভূমি BC-র একই পার্শ্বে অবস্থিত এবং এদের ক্ষেত্রফল সমান।
তাই \(\triangle \mathrm{BFC}\) ও \(\triangle \mathrm{BEC}\) একই সমান্তরালযুগল BC ও FE এর মধ্যে অবস্থিত।
\(\therefore \mathrm{FE} \| \mathrm{BC}\) (প্রমাণিত)
16. সমান ক্ষেত্রফলবিশিষ্ট ABCD ও AEFG সামন্তরিক আকারের ক্ষেত্র দুটির \(\angle \mathrm{A}\) সাধারণ এবং \(E, AB\) বাহুর উপর অবস্থিত। প্রমাণ করি যে, \(\mathrm{DE}|| \mathrm{FC}\)

প্রদত্ত : সমান ক্ষেত্রফলবিশিষ্ট ABCD ও AEFG দুটি সামান্তরিক, যাদের \(\angle \mathrm{A}\) সাধারণ এবং E বিন্দু AB বাহুর উপর অবস্থিত। D, E ও F, C যুক্ত করা হল।
প্রামাণ্য বিষয় : \(\mathrm{DE} \| \mathrm{FC}\)
অঙ্কন : D, F ও E, C যুক্ত করা হল।
প্রমাণ : যেহেতু, ABCD সামান্তরিক ও \(\triangle CDE\) একই ভূমি CD ও একই সমান্তরালযুগল CD ও AB-র মধ্যে অবস্থিত।
\(\therefore \triangle \mathrm{CDE}=\frac{1}{2}\) সামান্তরিক ABCD [\(\because\) একই ভূমি ও একই সমান্তরালযুগলের মধ্যে অবস্থিত ত্রিভুজের ক্ষেত্রফল সামান্তরিকের ক্ষেত্রফলের অর্ধেক]
আবার, \(\because\) AEFG সামান্তরিক ও \(\triangle \mathrm{DEF}\) একই ভূমি EF ও একই সমান্তরালযুগল EF ও AG-র মধ্যে অবস্থিত।
\(\therefore \triangle D E F=\frac{1}{2}\) সামান্তরিক \(AEFG \quad[\because \angle A B C=\angle A C B]\)
\(=\frac{1}{2}\) সামান্তরিক ABCD [\(\because\) স্বীকার অনুসারে, ABCD ও AEFG সামান্তরিকদ্বয়ের ক্ষেত্রফল সমান] \(\ldots(ii)\)
(i) ও (ii) হতে পাই, \(\triangle \mathrm{CDE}=\Delta \mathrm{DEF}\)
এখন, \(\because \triangle \mathrm{CDE}\) ও \(\triangle \mathrm{DEF}\) একই ভূমি DE-র একই পার্শ্বে অবস্থিত এবং এদের ক্ষেত্রফল সমান, সুতরাং \(\triangle \mathrm{CDE}\) ও \(\triangle \mathrm{DEF}\) একই সমান্তরালযুগল DE ও CF-র মধ্যে অবস্থিত।
\(\therefore D E \| F C\) (প্রমাণিত)
17. ABCD একটি সামান্তরিক এবং ABCE একটি চতুর্ভুজ। AC কর্ণ ABCE চতুর্ভুজ আকারের ক্ষেত্রটিকে দুটি সমান অংশে বিভক্ত করে। প্রমাণ করি যে, \(A C \| D E\)

প্রদত্ত : ABCD একটি সামান্তরিক ও ABCE একটি চতুর্ভুজ। AC কর্ণ ABCE চতুর্ভুজ আকারের ক্ষেত্রটিকে দুটি সমান অংশে বিভক্ত করে অর্থাৎ,
\(\triangle \mathrm{ABC}=\triangle \mathrm{ACE}\)
প্রামাণ্য বিষয় : \(A C \| D E\)
প্রমাণ : যেহেতু, সামান্তরিকের কর্ণ উহাকে সমান ক্ষেত্রফলবিশিষ্ট দুটি ত্রিভুজে বিভক্ত করে,
\(\therefore \triangle \mathrm{ABC}=\triangle \mathrm{ADC}\ldots(i)\)
আবার, \(\because\) AC কর্ণ ABCE চতুর্ভুজকে দুটি সমান অংশে বিভক্ত করে,
\(\therefore \triangle \mathrm{ABC}=\triangle \mathrm{ACE}\ldots(ii)\)
\(\therefore \triangle \mathrm{ADC}=\triangle \mathrm{ACE}\ldots\) (i) ও (ii) থেকে পাই,
আবার, \(\triangle \mathrm{ADC}\) ও \(\triangle \mathrm{ACE}\) একই ভূমি AC-র একই পার্শ্বে অবস্থিত এবং তাদের ক্ষেত্রফল সমান, সুতরাং \(\triangle \mathrm{ADC}\) ও \(\triangle \mathrm{ACE}\) একই সমান্তরালযুগল AC ও DE-র মধ্যে অবস্থিত।
\(\therefore A C \| D E\) (প্রমাণিত)
18. ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D; P এবং Q যথাক্রমে BC ও BA বাহুর উপর এমনভাবে অবস্থিত যে, \(\Delta B P Q=\frac{1}{2} \Delta A B C\) প্রমাণ করে যে, \(D Q \| P A\)

প্রদত্ত : \(\triangle \mathrm{ABC}\)-র BC বাহুর মধ্যবিন্দু D। P ও Q যথাক্রমে BC ও BA-র উপর দুটি বিন্দু এবং \(\triangle B P Q=\frac{1}{2} \triangle A B C\)
প্রামাণ্য বিষয় : \(D Q \| P A\)
প্রমাণ : যেহেতু, \(\triangle \mathrm{ABC}\)-র AD মধ্যমা,
\(\because \triangle \mathrm{ABD}=\triangle \mathrm{ACD}=\frac{1}{2} \triangle \mathrm{ABC}\) [\(\because\) ত্রিভুজের মধ্যমা উহাকে দুটি সমান ক্ষেত্রফলবিশিষ্ট ত্রিভুজে বিভক্ত করে] \(\ldots(i)\)
আবার, যেহেতু, \(\triangle \mathrm{BPQ}=\frac{1}{2} \triangle \mathrm{ABC}\ldots (ii)\)
(i) ও (ii) হতে পাই,
\(\triangle \mathrm{ABD}=\Delta \mathrm{BPQ} \)
বা, \(\triangle \mathrm{BDQ}+\triangle \mathrm{AQD}=\Delta \mathrm{BDQ}+\triangle \mathrm{PQD} \)
বা, \(\triangle \mathrm{AQD}=\Delta \mathrm{PQD}\)
আবার, \(\triangle \mathrm{AQD}\) ও \(\triangle \mathrm{PQD}\) একই ভূমি QD-র একই পার্শ্বে অবস্থিত এবং ক্ষেত্রফল সমান।
\(\therefore \triangle \mathrm{AQD}\) ও \(\triangle \mathrm{PQD}\) একই সমান্তরালযুগল QD ও AP-র মধ্যে অবস্থিত।
\(\therefore D Q \| P A\) (প্রমাণিত)
19. ABCD সামান্তরিকের AB, BC, CD এবং DA বাহুর মধ্যবিন্দু যথাক্রমে E, F, G ও H; প্রমাণ করি যে, (i) EFGH একটি সামান্তরিক (ii) EFGH সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফলের অর্ধেক।

প্রদত্ত : ABCD সামান্তরিকের AB, BC, CD ও DA বাহুর মধ্যবিন্দু যথাক্রমে E, F, G ও H।
প্রামাণ্য বিষয় : (i) EFGH একটি সামান্তরিক।
(ii) সামান্তরিক \(\mathrm{EFGH}=\frac{1}{2}\) সামান্তরিক ABCD।
অঙ্কন : A, C এবং E, G যুক্ত করা হল।
প্রমাণ : \(\triangle \mathrm{ADC}\) এর AD-র মধ্যবিন্দু H এবং CD-র মধ্যবিন্দু G।
\(\therefore \mathrm{HG} \| \mathrm{AC}\) এবং \(H G=\frac{1}{2} A C\ldots(i)\) [\(\because\) ত্রিভুজের যে-কোনো দুই বাহুর মধ্যবিন্দুর সংযোজক রেখাংশ তৃতীয় বাহুর সমান্তরাল ও অর্ধেক]
আবার, \(\triangle A B C\)-র AB-র মধ্যবিন্দু E এবং BC-র মধ্যবিন্দু F।
\(\therefore \mathrm{EF} \| \mathrm{AC}\) এবং \(E F=\frac{1}{2} A C\ldots(2)\) [\(\because\) ত্রিভুজের যে-কোনো দুই বাহুর মধ্যবিন্দুর সংযোজক রেখাংশ তৃতীয় বাহুর সমান্তরাল ও অর্ধেক]
(1) ও (2) থেকে পাই, \(H G \| E F\) এবং HG = EF
\(\therefore\) EFGH একটি সামান্তরিক [(i) নং প্রমাণিত]
[\(\because\) কোনো চতুর্ভুজের একজোড়া বিপরীত বাহু পরস্পর সমান ও সমান্তরাল হলে চতুর্ভুজটি সামান্তরিক হয়]
আবার, \(\because\) ABCD একটি সামান্তরিক
\(\therefore\) AB = DC
বা, \(\frac{1}{2} A B=\frac{1}{2} D C\)
এবং, \(A B \| D C\)
\(\therefore \mathrm{AE} \| \mathrm{DG}\)
\(\therefore A E=D G\)
\(\therefore\) AEGD একটি সামান্তরিক [\(\because\) কোনো চতুর্ভুজের একজোড়া বিপরীত বাহু পরস্পর সমান ও সমান্তরাল হলে চতুর্ভুজটি সামান্তরিক হয়]
এখন, AEGD সামান্তরিক ও \(\triangle \mathrm{GHE}\) একই ভূমি EG ও একই সমান্তরালযুগল EG ও AD-র মধ্যে অবস্থিত।
\(\therefore \triangle \mathrm{GHE}=\frac{1}{2}\) সামান্তরিক \(AEGD\ldots (3)\)
আবার, BCGE একটি সামান্তরিক ও \(\triangle E F G\) একই ভূমি GE ও একই সমান্তরালযুগল \(B C \| G E\)-র মধ্যে অবস্থিত।
\(\therefore \triangle E F G=\frac{1}{2}\) সামান্তরিক \(BCGE \ldots(4) \)
\(\therefore\) (3) ও (4) যোগ করে পাই,
\(\Delta \mathrm{GHE}+\Delta \mathrm{EFG}=\frac{1}{2}\) সামান্তরিক \(AEGD +\frac{1}{2}\) সামান্তরিক BCGE
বা, সামান্তরিক EFGH
\(=\frac{1}{2}\) (সামান্তরিক AEGD + সামান্তরিক BCGE)
\(\therefore\) সামান্তরিক \(\mathrm{EFGH}=\frac{1}{2}\) সামান্তরিক ABCD [(ii) প্রমাণিত]
20. ABCD ট্রাপিজিয়মের \(A B \| D C\) এবং BC বাহুর মধ্য বিন্দু E; প্রমাণ করি যে, AED ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল \(=\frac{1}{2} \times A B C D\) ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল।

প্রদত্ত : ABCD ট্রাপিজিয়ামের \(A B \| D C\) এবং BC বাহুর মধ্যবিন্দু E;
প্রামাণ্য বিষয় : \(\triangle \mathrm{ADE}=\frac{1}{2} \times\) ট্রাপিজিয়াম ABCD
অঙ্কন : E বিন্দু দিয়ে AD-র সমান্তরাল সরলরেখা অঙ্কন করল, যা AB-কে P বিন্দুতে এবং বর্ধিত DC -কে Q বিন্দুতে ছেদ করল।
প্রমাণ : \(\triangle \mathrm{CEQ}\) এবং \(\triangle \mathrm{PEB}\)-র
(i) \(\angle \mathrm{QEC}=\angle \mathrm{PEB}\quad\) [বিপ্রতীপ কোণ]
(ii) \(CE = BE\quad [\because E, BC\)-র মধ্যবিন্দু]
(iii) \(\angle \mathrm{QCE}=\angle \mathrm{EBP}\)
\(\quad\quad[\because \mathrm{DQ} \| \mathrm{AB}\) এবং \(BC\) ভেদক \(\therefore \angle Q C B=\) একান্তর \(\angle C B P]\)
\(\therefore \triangle C E Q \cong \triangle \mathrm{PEB}\quad\) [A-S-A শর্তে]
\(\therefore \triangle \mathrm{CEQ}=\triangle \mathrm{PEB}\)
এখন, ট্রাপিজিয়াম ABCD = পঞ্চভুজ \(APECD + \triangle PEB\)
= পঞ্চভুজ \(A P E C D+\triangle C E Q\)
= সামান্তরিক \(APQD\ldots(i)\)
আবার, \(\because \triangle \mathrm{AED}\) ও সামান্তরিক APQD একই ভূমি AD ও একই সমান্তরালযুগল AD ও PQ-র মধ্যে অবস্থিত।
\(\therefore \triangle \mathrm{AED}=\frac{1}{2} \times\) সামান্তরিক APQD [\(\because\) একই ভূমি ও একই সমান্তরালযুগলের মধ্যে অবস্থিত ত্রিভুজের ক্ষেত্রফল সামান্তরিকের ক্ষেত্রফলের অর্ধেক]
\(=\frac{1}{2} \times\) ট্রাপিজিয়াম ABCD [(i) হতে পাই] (প্রমাণিত)
21. বহু বিকল্পীয় প্রশ্ন (M.C.Q) :
(i) \(\Delta\) ABC এর BC, CA ও AB বাহুর মধ্যবিন্দু যথাক্রমে D, E ও F; যদি \(\triangle \mathrm{ABC}=16\) বর্গসেমি. হয় তাহলে FBCE ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল
(a) 40 বর্গসেমি (b) 8 বর্গসেমি (c) 12 বর্গসেমি (d) 100 বর্গসেমি
(a) 40 বর্গসেমি (b) 8 বর্গসেমি (c) 12 বর্গসেমি (d) 100 বর্গসেমি

যেহেতু, \(\triangle \mathrm{ABC}\)-র BC, CA ও AB বাহুর মধ্যবিন্দু D, E, F
\(\therefore\) F, D; D, E ও E, F যুক্ত করার ফলে যে চারটি ত্রিভুজ উৎপন্ন হয়, তাদের প্রতিটির ক্ষেত্রফল সমান।
\(\therefore \triangle \mathrm{AFE}=\triangle \mathrm{FDE}=\triangle \mathrm{FBD}=\Delta \mathrm{DEC}=\frac{1}{4} \times \triangle \mathrm{ABC}\)
\(=\left(\frac{1}{4} \times 16\right)\) বর্গসেমি = 4 বর্গসেমি
এখন, ট্রাপিজিয়াম FBCE আকার ক্ষেত্রের ক্ষেত্রফল
\(=\Delta \mathrm{FBD}+\Delta \mathrm{FDE}+\Delta \mathrm{DEC}\)
= (4 + 4 + 4) বর্গসেমি = 12 বর্গসেমি
নবম শ্রেণী কষে দেখি 12 || ক্ষেত্রফল সংক্রান্ত উপপাদ্য || Class 9 Chapter 12 || Ganit Prakash Class 9 Math Solution || West Bengal Board Class 9 Math || Class 9 Chapter 12 koshe dekhi 12
(ii) A, B, C, D যথাক্রমে PQRS সামান্তরিকের PQ, QR, RS, SP বাহর মধ্যবিন্দু। PQRS সামান্তারক আকার ক্ষেত্রের ক্ষেত্রফল = 36 বর্গ সেমি. হলে ABCD ক্ষেত্রের ক্ষেত্রফল
(a) 24 বর্গ সেমি. (b) 18 বর্গ সেমি. (c) 30 বর্গ সেমি. (d) 36 বর্গ সেমি.
(a) 24 বর্গ সেমি. (b) 18 বর্গ সেমি. (c) 30 বর্গ সেমি. (d) 36 বর্গ সেমি.

অঙ্কন : A, C যুক্ত করা হল।
APSC চতুর্ভুজের PA = SC \(\quad\left[\because \mathrm{PQ}=\mathrm{SR} \therefore \frac{1}{2} \mathrm{PQ}=\frac{1}{2} \mathrm{SR}\right]\)
এবং \(PA \| SC \quad[\because PQRS\) সামান্তরিক\(]\)
\(\therefore\) APSC একটি সামান্তরিক।
এখন \(\triangle \mathrm{ADC}\) এবং সামান্তরিক APSC একই ভূমি AC ও একই সমান্তরালযুগল AC ও PS-র মধ্যে অবস্থিত।
\(\therefore \triangle \mathrm{ADC}=\frac{1}{2}\) সামান্তরিক \(APSC\ldots(i)\)
অনূরপে, \(\triangle \mathrm{ABC}=\frac{1}{2}\) সামান্তরিক \(AQRC \ldots(ii)\)
\(\therefore\) (i) ও (ii) যোগ করে পাই,
\(\triangle \mathrm{ADC}+\triangle \mathrm{ABC}=\frac{1}{2}\) সামান্তরিক \(APSC+\frac{1}{2}\) সামান্তরিক \(AQRC\)
বা, সামান্তরিক \(A B C D=\frac{1}{2} \times\) সামান্তরিক PQRS
\(=\left(\frac{1}{2} \times 36\right)\) বর্গসেমি = 18 বর্গসেমি
(iii) ABCD সামান্তরিকের ভিতরের যে কোনো একটি বিন্দু। \(\Delta \mathrm{AOB}+\Delta \mathrm{COD}\) = 16 বর্গ সেমি. হলে, ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল
(a) 8 বর্গ সেমি. (b) 4 বর্গ সেমি. (c) 32 বর্গ সেমি. (d) 64 বর্গ সেমি.
(a) 8 বর্গ সেমি. (b) 4 বর্গ সেমি. (c) 32 বর্গ সেমি. (d) 64 বর্গ সেমি.

অঙ্কন : O বিন্দু দিয়ে \(P Q \| D C(\| A B)\) অঙ্কন করা হল।
যেহেতু, APQB চতুর্ভুজের \(A P \| Q B\) এবং \(\mathrm{AB} \| \mathrm{QP}\)
\(\therefore\triangle APQB \) একটি সামান্তরিক।
\(\therefore \triangle \mathrm{AOB}\) ও সামান্তরিক APQB একই ভূমি AB ও একই সমান্তরালযুগল AB ও QP-র মধ্যে অবস্থিত।
\(\therefore \triangle \mathrm{AOB}=\frac{1}{2}\) সামান্তরিক \(APQB\ldots(i)\)
অনুরূপে, \(\triangle \mathrm{DOC}=\frac{1}{2}\) সামান্তরিক \(PQCD \ldots(ii)\)
\(\therefore\) (i) ও (ii) যোগ করে পাই, \(\triangle A O B+\triangle D O C\)
\(=\frac{1}{2}\) সামান্তরিক \(\mathrm{APQB}+\frac{1}{2}\) সামান্তরিক PQCD
\(\therefore \frac{1}{2}\) (সামান্তরিক APQB + সামান্তরিক PQCD)
\(=\triangle \mathrm{AOB}+\Delta \mathrm{COD}\)
বা, \(\frac{1}{2} \times\) সামান্তরিক ABCD = 16 বর্গসেমি [প্রদত্ত]
\(\therefore\) সামান্তরিক ABCD = 32 বর্গসেমি
(iv) ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D, BD বাহুর মধ্যবিন্দু E এবং AE-এর মধ্যবিন্দু O; BOE ত্রিভুজাকার, ক্ষেত্রের ক্ষেত্রফল
(a) \(\frac{1}{3} \times A B C\) ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
(b) \(\frac{1}{4} \times A B C\) ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
(C) \(\frac{1}{6} \times A B C\) ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
(d) \(\frac{1}{8} \times A B C\) ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
(a) \(\frac{1}{3} \times A B C\) ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
(b) \(\frac{1}{4} \times A B C\) ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
(C) \(\frac{1}{6} \times A B C\) ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
(d) \(\frac{1}{8} \times A B C\) ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল

অঙ্কন : A, D যুক্ত করা হল।
যেহেতু মধ্যমা ত্রিভুজকে দুটি সমান ক্ষেত্রফলবিশিষ্ট ত্রিভুজে বিভক্ত করে।
\(\therefore\) AD মধ্যমা \(\triangle A B C\)-কে দুটি সমান ক্ষেত্রফলবিশিষ্ট ত্রিভুজে বিভক্ত করবে।
\(\therefore \triangle \mathrm{ADB}=\frac{1}{2} \times \triangle \mathrm{ABC}\ldots(i)\)
আবার, \(\because \triangle \mathrm{ADB}\)-র \(AE\) মধ্যমা,
\(\therefore \triangle \mathrm{ABE}=\frac{1}{2} \times \triangle \mathrm{ADB}\)
\(=\frac{1}{2} \times \frac{1}{2} \times \triangle \mathrm{ABC}\quad\) [(i) হতে পাই]
\(=\frac{1}{4} \triangle \mathrm{ABC}\ldots (ii)\)
আবার, \(\because \triangle \mathrm{ABE}\)-র \(BO\) মধ্যমা,
\(\therefore \triangle \mathrm{BOE}=\frac{1}{2} \times \triangle \mathrm{ABE}\)
\(=\frac{1}{2} \times \frac{1}{4} \times \triangle \mathrm{ABC}\quad\) [(ii) হতে পাই]
\(=\frac{1}{8} \times \triangle \mathrm{ABC}\)
(v) একটি সামান্তরিক আকারের ক্ষেত্রে, একটি আয়তক্ষেত্র এবং একটি ত্রিভুজাকার ক্ষেত্র একই ভূমি ও একই সমান্তরাল যুগলের মধ্যে অবস্থিত এবং তাদের ক্ষেত্রফল P, R ও T হলে,
(a) \(P = R = 2T\) (b) \(P = R= \frac{T}{2}\)
(c) \(2P = 2R = T\) (d) \(P = R = T\)
(a) \(P = R = 2T\) (b) \(P = R= \frac{T}{2}\)
(c) \(2P = 2R = T\) (d) \(P = R = T\)

যেহেতু, একই ভূমি ও একই সমান্তরালযুগলের মধ্যে অবস্থিত একটি সামান্তরিক ও একটি আয়তক্ষেত্রের ক্ষেত্রফল সমান এবং ত্রিভুজের ক্ষেত্রফল সামান্তরিক ও আয়তক্ষেত্রের ক্ষেত্রফলের অর্ধেক।
\(\therefore\) সামান্তরিকের ক্ষেত্রফল P, আয়তক্ষেত্রের ক্ষেত্রফল R এবং ত্রিভুজের ক্ষেত্রফল T হলে,
\(T=\frac{P}{2}=\frac{R}{2}\)
বা, \(2 \mathrm{~T}=\mathrm{P}=\mathrm{R}\)
\(\therefore P=R=2 T\)
22. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন :
(i) ABCD সামান্তরিকের D বিন্দু থেকে AB বাহুর উপর লম্ব DE এবং B বিন্দু থেকে AD বাহুর উপর লম্ব BF; AB = 10 সেমি, AD = 8 সেমি এবং DE = 6 সেমি. হলে, BF এর দৈর্ঘ্য কত তা লিখি?
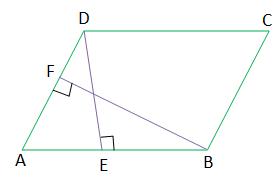
ABCD সামান্তরিকের ক্ষেত্রফল \(\mathrm{AB} \times \mathrm{DE}\), যখন AB ভূমি ও DE উচ্চতা।
আবার, যদি AD ভূমি ও BF উচ্চতা ধরা হয় তবে ABCD সামান্তরিকের ক্ষেত্রফল \(A D \times B F\)
\(\therefore A B \times D E=A D \times B F\)
বা, \(10 \times 6=8 \times B F\)
বা, \(\mathrm{BF}=\frac{10 \times 6}{p8}=7.5\)
\(\therefore\) BF-র দৈর্ঘ্য 7.5 সেমি।
(ii) ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল 100 বর্গ একক; BC বাহুর মধ্যবিন্দু P; ABP ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল কত তা লিখি।

\(\triangle \mathrm{ABP}=\frac{1}{2} \times \triangle \mathrm{ABC}\) [\(\because\) ত্রিভুজের মধ্যমা ত্রিভুজকে দুটি সমান ক্ষেত্রফল বিশিষ্ট ত্রিভুজে বিভক্ত করে]
\(=\frac{1}{2} \times \frac{1}{2} \times\) সামান্তরিক ABCD
[\(\because\) সামান্তরিকের কর্ণ সামান্তরিককে দুটি সমান ক্ষেত্রফলবিশিষ্ট ত্রিভুজে বিভক্ত করে।]
\(=\left(\frac{1}{4} \times 100\right)\) বর্গএকক [\(\therefore\) ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল 100 বর্গএকক]
= 25 বর্গ একক
\(\therefore \triangle \mathrm{ABP}\) ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল 25 বর্গএকক।
(iii) ABC ব্রিজের AD মধ্যমা এবং AC বাহুর উপর P এমন একটি বিন্দু থাকে \(\Delta A D P\) এর ক্ষেত্রফল : ABD অর ক্ষেত্রফল 2: 3 হয়। \(\Delta P D C\) -এর ক্ষেত্রফল : \(\Delta A B C\) এর ক্ষেত্রফল কত তা লিখি।

\(\because \triangle \mathrm{ADP}\)-র ক্ষেত্রফল \(: \triangle \mathrm{ABD}\)-র ক্ষেত্রফল \(= 2 : 3\)
মনে করি, \(\triangle \mathrm{ADP}\)-র ক্ষেত্রফল \(2x\) বর্গএকক এবং \(\triangle \mathrm{ABD}\)-র ক্ষেত্রফল \(3x\) বর্গএকক [\(x\) যেখানে আনুপাতিক ধ্রুবক]
যেহেতু, ত্রিভুজের মধ্যমা উহাকে দুটি সমান ক্ষেত্রফলবিশিষ্ট ত্রিভুজে বিভক্ত করে,
\(\therefore \triangle \mathrm{ADC}=\triangle \mathrm{ABD}\)
\(= 3x\) বর্গএকক
\(\because \Delta \mathrm{ADC}=3 x\) বর্গএকক
বা, \(\Delta \mathrm{ADP}+\Delta \mathrm{DPC}=3 x\) বর্গএকক
বা, \(2x\) বর্গএকক \(+\Delta \mathrm{DPC}=3 x\) বর্গএকক
বা, \(\triangle \mathrm{DPC}=(3 x-2 x)\) বর্গএকক \(= x\) বর্গএকক
এখন, \(\triangle \mathrm{PDC}\)-এর ক্ষেত্রফল \(: ABC\) এর ক্ষেত্রফল
\(=x:(3 x+3 x)=x: 6 x=1: 6\)
\(\therefore \triangle \mathrm{PDC}\) ও \(\triangle \mathrm{ABC}\)-র ক্ষেত্রফলের অনুপাত \(1 : 6\)
(iv) ABDE একটি সামান্তরিক। F, ED বাহুর মধ্যবিন্দু। ABD ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল 20 বর্গ সেমি. হলে, AEF ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল কত তা লিখি।

যেহেতু, ABDE সামান্তরিকের কর্ণ AD, উহাকে সমান ক্ষেত্রফলবিশিষ্ট দুটি ত্রিভুজে বিভক্ত করে।
\(\therefore \triangle \mathrm{ADE}=\triangle \mathrm{ABD}=20\) বর্গসেমি
আবার, \(\because \triangle \mathrm{ADE}\)-র AF মধ্যমা,
\(\therefore \triangle \mathrm{AEF}=\frac{1}{2} \times \triangle \mathrm{ADE}\) [\(\because\) ত্রিভুজের মধ্যমা ত্রিভুজকে দুটি সমান ক্ষেত্রফলবিশিষ্ট ত্রিভুজে বিভক্ত করে]
\(=\frac{1}{2} \times 20\) বর্গসেমি = 10 বর্গসেমি
\(\therefore \triangle \mathrm{AEF}\) ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল 10 বর্গসেমি।
(v) \(PORS\) একটি সামান্তরিক। \(X\) এবং \(Y\) যথাক্রমে \(PQ\) এবং \(SR\) বাহুর মধ্যবিন্দু। কর্ণ \(SQ\) যুক্ত করি। সামান্তরিক \(XQRY\) আকার ক্ষেত্রের ক্ষেত্রফল : \(QSR\) ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল কত তা লিখি।

যেহেতু, \(X\) ও \(Y\) যথাক্রমে PQ ও SR-র মধ্যবিন্দু।
\(\therefore\) সামান্তরিক \(X Q R Y=\frac{1}{2} \times\) সামান্তরিক \(PQRS\ldots(i)\)
আবার, \(\because\) SQ, সামান্তরিক PQRS-র কর্ণ,
\(\therefore \triangle \mathrm{QRS}=\frac{1}{2} \times\) সামান্তরিক \(PQRS\ldots(ii) \)
\(\therefore\) সামান্তরিক \(XQRY : \triangle Q R S\)
\(=\frac{1}{2} \times\) সামান্তরিক \(PQRS : \frac{1}{2} \times\) সামান্তরিক PQRS
\(= 1 : 1\quad\) [(i) ও (ii) হতে পাই]
নবম শ্রেণী কষে দেখি 12 || ক্ষেত্রফল সংক্রান্ত উপপাদ্য || Class 9 Chapter 12 || Ganit Prakash Class 9 Math Solution || West Bengal Board Class 9 Math || Class 9 Chapter 12 koshe dekhi 12
এই Page টি বা এই Website টির কোন প্রকার বিষয়বস্তু কপি করা বা সম্পাদনা করা নিষিদ্ধ। ভারতীয় Copywright আইন 1957 এর ধারা 63 অনুযায়ী, এই ফাইলটির সমস্ত অধিকার 'ছাত্র মিত্র Mathematics' অ্যাপ দ্বারা সংরক্ষিত। ছাত্র মিত্রের অনুমতি ছাড়া, এই Page টি বা এই Website টির কোন প্রকার বিষয়বস্তু কপি করা বা সম্পাদনা করা আইনত দন্ডনীয় অপরাধ। কেউ ছাত্র মিত্রের অনুমতি ছাড়া, এই Page টি বা এই Website টির কোন প্রকার বিষয়বস্তু কপি বা সম্পাদনা করলে ছাত্র মিত্র কতৃপক্ষ তার বিরুদ্ধে সকল প্রকার কঠোর আইনি পদক্ষেপ করবে।
West Bengal Board of Secondary Education Official Site
Class 8 : গণিত প্রভা (অষ্টম শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali.
Class 7 : গণিত প্রভা (সপ্তম শ্রেণি) বইয়ের সমস্ত সমাধান
www.wbresults.nic.in Official
Class 10 : মাধ্যমিক গণিত প্রকাশ (দশম শ্রেণি) বইয়ের সমস্ত সমাধান Class 10 Maths Solution WBBSE Bengali
Class 6 : গণিত প্রভা (ষষ্ঠ শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali
Class 9 : গণিত প্রকাশ (নবম শ্রেণি) বইয়ের সমাধান Maths Solution WBBSE Bengali
আজই Install করুন Chatra Mitra
Class 8 : গণিত প্রভা (অষ্টম শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali.
Class 7 : গণিত প্রভা (সপ্তম শ্রেণি) বইয়ের সমস্ত সমাধান
www.wbresults.nic.in Official
Class 10 : মাধ্যমিক গণিত প্রকাশ (দশম শ্রেণি) বইয়ের সমস্ত সমাধান Class 10 Maths Solution WBBSE Bengali
Class 6 : গণিত প্রভা (ষষ্ঠ শ্রেণি) বইয়ের সমস্ত সমাধান Maths solutions for WBBSE in Bengali
Class 9 : গণিত প্রকাশ (নবম শ্রেণি) বইয়ের সমাধান Maths Solution WBBSE Bengali
আজই Install করুন Chatra Mitra



