প্রদত্ত : $\triangle \mathrm{ABC}$-র BC-র মধ্যবিন্দু D; D বিন্দু দিয়ে CA ও BA-এর সমান্তরাল সরলরেখাংশ BA ও CA বাহুকে যথাক্রমে E ও F বিন্দুতে ছেদ করে। E, F যুক্ত করা হল।
প্রমাণ করতে হবে যে, $E F=\frac{1}{2} B C$
প্রমাণ : $\triangle \mathrm{ABC}$-এর BC বাহুর মধ্যবিন্দু D এবং DE || CA
$\therefore$ E, AB-এর মধ্যবিন্দু। [$\because$ ত্রিভুজের যে-কোনো একটি বাহুর মধ্যবিন্দু দিয়ে অঙ্কিত দ্বিতীয় বাহুর সমান্তরাল সরলরেখা তৃতীয় বাহুকে মধ্যবিন্দুতে ছেদ করে]
আবার একইভাবে,
$\triangle \mathrm{ABC}$-এর BC বাহুর মধ্যবিন্দু D এবং DF || AB
$\therefore$ F, AC-এর মধ্যবিন্দু। [একই কারণে]
এখন $\triangle \mathrm{ABC}$-এর AB-এর মধ্যবিন্দু E এবং AC-এর মধ্যবিন্দু F।
$\therefore E F=\frac{1}{2} B C$ (প্রমাণিত) [$\because$ ত্রিভুজের যে-কোনো দুই বাহুর মধ্যবিন্দুর সংযোজক রেখাংশ তৃতীয় বাহুর অর্ধেক।]

প্রদত্ত : $\triangle A B C$-র AB ও AC-র উপর যথাক্রমে D ও E এমনভাবে অবস্থিত যাতে $A D=\frac{1}{4} A B$ এবং $A E=\frac{1}{4} A C$ হয়।
প্রামাণ্য বিষয় : প্রমাণ করতে হবে যে, (i) $DE \| BC$ এবং (ii) $D E=\frac{1}{4} B C$
অঙ্কন : AB-এর মধ্যবিন্দু F এবং AC-র মধ্যবিন্দু G নিয়ে F, G যুক্ত করা হল।
প্রমাণ : $\because \triangle \mathrm{ABC}$-র AB-র মধ্যবিন্দু F এবং AC-র মধ্যবিন্দু G
$\therefore FG \| BC$ এবং $F G=\frac{1}{2} B C$ [$\because$ ত্রিভুজের যে-কোনো দুই বাহুর মধ্যবিন্দুর সংযোজক রেখাংশ তৃতীয় বাহুর সমান্তরাল ও অর্ধেক]
আবার, $\because$ F, AB-র মধ্যবিন্দু এবং $A D=\frac{1}{4} A B$
$\therefore$ D, AF-র মধ্যবিন্দু।
আবার, $\because$ G, AC-র মধ্যবিন্দু এবং $A E=\frac{1}{4} A C$
$\therefore$ E, AG-এর মধ্যবিন্দু।
এখন $\triangle \mathrm{AFG}$-এর AF-এর মধ্যবিন্দু D এবং AG-এর মধ্যবিন্দু E
$\therefore DE \| FG$ এবং $D E=\frac{1}{2} F G$
$\therefore FG \| BC$ এবং $DE \| FG$
$\therefore DE \| BC\quad$ [(i) নং প্রমাণিত]
আবার, $\because F G=\frac{1}{2} B C$ এবং $D E=\frac{1}{2} F G$
$\therefore D E=\frac{1}{2} \cdot \frac{1}{2} B C$
$\therefore D E=\frac{1}{4} B C\quad$ [(ii) নং প্রমাণিত]

প্রদত্ত : $\triangle \mathrm{PQR}$-র QR-র মধ্যবিন্দু $X$ এবং PQ-এর মধ্যবিন্দু Z. QP কে S পর্যন্ত এরূপে বর্ধিত করা হল যেন SP = PZ হয়। $S, X$ যুক্ত করা হল যা, PR -কে Y বিন্দুতে ছেদ করে।
প্রামাণ্য বিষয় : $P Y=\frac{1}{4} P R$
অঙ্কন : $X, Z$ যুক্ত করা হল।
প্রমাণ : $\because$ QP ও QR-র মধ্যবিন্দু যথাক্রমে Z ও $X$
$\therefore Z X \| P R$ এবং $Z X=\frac{1}{2} P R$ [$\because$ ত্রিভুজের যে-কোনো দুই বাহুর মধ্যবিন্দুর সংযোজক রেখাংশ তৃতীয় বাহুর সমান্তরাল ও অর্ধেক]
আবার, SZ-র মধ্যবিন্দু P এবং $PY \| Z X$ [$\because$ PY ও PR একই সরলরেখায় আছে]
$\therefore SX$-র মধ্যবিন্দু $Y$
$\therefore P Y=\frac{1}{2} Z X=\frac{1}{2} \times \frac{1}{2} P R\quad\left[\because Z X=\frac{1}{2} P R\right]$
$\therefore P Y=\frac{1}{4} P R$ (প্রমাণিত)

ধরা যাক, ABCD একটি সামান্তরিকের চারটি বাহু AB, BC, CD ও DA বাহুর মধ্যবিন্দু যথাক্রমে P, Q, R ও S।
P, Q; Q, R; R, S ও S, P যুক্ত করা হল এবং PQRS একটি চতুর্ভুজ গঠিত হল।
প্রামাণ্য বিষয় : PQRS একটি সামান্তরিক।
অঙ্কন : BD কর্ণ অঙ্কন করা হল।
প্রমাণ : $\triangle \mathrm{ABD}$-র AB ও AD-র মধ্যবিন্দু যথাক্রমে P ও S
$\therefore$ $P S \| B D$ এবং $P S=\frac{1}{2} B D$
আবার, $\triangle \mathrm{BCD}$-র BC ও CD-র মধ্যবিন্দু যথাক্রমে Q ও R
$\therefore$ $\mathrm{QR} \| \mathrm{BD}$ এবং $Q R=\frac{1}{2} B D$
$\because P S \| B D$ এবং $\mathrm{QR} \| \mathrm{BD}$
$\because PS\| QR$
আবার, $\because P S=\frac{1}{2} B D$ এবং $\mathrm{QR}=\frac{1}{2} \mathrm{BD}$
$\therefore$ PS = QR
$\therefore$ PQRS চতুর্ভুজের $PS \| QR$ এবং PS = QR
অতএব, PQRS চতুর্ভুজটি একটি সামান্তরিক। (প্রমাণিত)
[$\because$ কোনো চতুর্ভুজের একজোড়া বিপরীত বাহু সমান ও সমান্তরাল হলে চতুর্ভুজটি একটি সামান্তরিক হবে।]

ধরা যাক, ABCD একটি আয়তাকার চিত্র (AD > AB) যার AB, BC, CD ও DA বাহুর মধ্যবিন্দু যথাক্রমে P, Q, R ও S।
P, Q; Q, R; R, S; S, P বিন্দুগুলি ক্রমান্বয়ে যুক্ত করলে PQRS চতুর্ভুজটি উৎপন্ন হল।
প্রামাণ্য বিষয় : PQRS একটি রম্বস কিন্তু বর্গক্ষেত্র নয়।
অঙ্কন : P, R ও Q, S যুক্ত করা হল।
প্রমাণ : $\triangle \mathrm{APS}$ ও $\triangle \mathrm{BPQ}$-র
(i) AP = BP$\quad$ [P, AB-র মধ্যবিন্দু]
(ii) $\angle \mathrm{PAS}=\angle \mathrm{PBQ}\left(=90^{\circ}\right)\quad$ [$\because ABCD$ একটি আয়তক্ষেত্র]
(ii) $AS = BQ \quad[ \because A D=B C \therefore \frac{1}{2} A D=\frac{1}{2} B C]$
$\therefore \triangle \mathrm{APS} \cong \triangle \mathrm{BPQ}\quad$ [S-A-S শর্তানুসারে]
$\therefore PS = PQ\quad$ [সর্বসম ত্রিভুজের অনুরূপ বাহু]
অনুরূপে, $\triangle PBQ$ ও $\triangle RCQ$ থেকে পাই, PQ = QR
$\triangle RCQ$ ও $\triangle RDS$ থেকে পাই, QR = RS
এবং $\triangle RDS$ ও $\triangle APS$ থেকে পাই, RS = PS
$\therefore$ PQRS চতুর্ভুজের PS = PQ = QR = RS
$\therefore$ PQRS চতুর্ভুজটি একটি রম্বস।
APRD চতুর্ভুজের AP = DR [$\because$ AB = DC এবং P ও R যথাক্রমে AB ও DC-র মধ্যবিন্দু]
$AP \| DR$ এবং $\angle \mathrm{PAD}=90^{\circ}\quad$[$\because$ ABCD আয়তক্ষেত্র]
$\therefore$ APRD একটি আয়তাকার চিত্র
$\therefore$ AD = PR
অনুরূপে, ABQS থেকে পাওয়া যায় AB = QS
$\because AD > AB$
$\therefore PR > QS$
$\because$ PQRS রম্বসের কর্ণদ্বয় (PR ও QS) অসমান,
$\therefore$ ইহা বর্গাকার চিত্র নয়। (প্রমাণিত)

ধরা যাক, ABCD বর্গক্ষেত্রের AB, BC, CD ও DA বাহুর মধ্যবিন্দু যথাক্রমে P, Q, R ও S; P, Q; Q, R; R, S; S, P কে ক্রমান্বয়ে যুক্ত করলে PQRS চতুর্ভুজটি গঠিত হয়।
প্রামাণ্য বিষয় : PQRS একটি বর্গাকার চিত্র।
প্রমাণ : $\triangle \mathrm{APS}$ ও $\triangle \mathrm{BPQ}$-র
(i) $AP= PB\quad [\because P, AB$-এর মধ্যবিন্দু$]$
(ii) $\angle \mathrm{PAS}=\angle \mathrm{PBQ}\left(=90^{\circ}\right)$
(iii) $AS =BQ\quad [\therefore ABCD$ একটি বর্গক্ষেত্র$]$
$\therefore \triangle \mathrm{APS} \cong \triangle \mathrm{BPQ}\quad [\because S-A-S$ শর্তানুসারে$]$
$\therefore PS = PQ\quad[\because$ সর্বসম ত্রিভুজের অনুরূপ বাহু$]$
অনুরূপভাবে, $\triangle \mathrm{BPQ}$ ও $\triangle \mathrm{CRQ }$ থেকে পাই, $PQ = QR$
$\triangle \mathrm{CRQ}$ ও $\Delta \mathrm{DRS}$ থেকে পাই, $QR=RS$
এবং $\triangle \mathrm{DRS}$ ও $\Delta \mathrm{APS}$ থেকে পাই, $RS=PS$
$\because PQRS$ চতুর্ভুজের PS = PQ = QR = RS
$\because$ PQRS একটি রম্বস।
$\therefore ABCD$ বর্গক্ষেত্র,
$\therefore A B=A D$
বা, $\frac{1}{2} A B=\frac{1}{2} \mathrm{AD}$
$\therefore A P=A S$
$\therefore \angle A S P=\angle A P S$
$\because \angle P A S=90^{\circ}$
$\therefore \angle A S P=45^{\circ}$
অনুরুপভাবে, $\angle D S R=45^{\circ}$
$\therefore \angle \mathrm{PSR}=180^{\circ}-(\angle \mathrm{ASP}+\angle \mathrm{DSR})$
$=180^{\circ}-\left(45^{\circ}+45^{\circ}\right)=90^{\circ}$
$\therefore$ PQRS রম্বসের একটি কোণ $\angle \mathrm{PSR}=90^{\circ}$
$\therefore$ PQRS একটি বর্গাকার চিত্র। (প্রমাণিত)

ধরা যাক, ABCD একটি রম্বস যার AB, BC, CD ও DA বাহুর মধ্যবিন্দুগুলি যথাক্রমে P, Q, R ও S।
P, Q, R, S পরপর যুক্ত করার ফলে PQRS একটি চতুর্ভুজ উৎপন্ন হল।
প্রামাণ্য বিষয় : PQRS একটি আয়তাকার চিত্র।
অঙ্কন : BD যুক্ত করা হল।
প্রমাণ : $\triangle \mathrm{ABD}$-র AB ও AD-র মধ্যবিন্দু যথাক্রমে P ও S
$\therefore \mathrm{PS} \| \mathrm{BD}$ এবং $PS =\frac{1}{2} \mathrm{BD}\ldots(i)$ [$\because$ ত্রিভুজের যে-কোনো দুটি বাহুর মধ্যবিন্দুর সংযোজক রেখাংশ তৃতীয় বাহুর সমান্তরাল ও অর্ধেক]
আবার $\triangle \mathrm{BCD}$-এর BC ও CD-র মধ্যবিন্দু যথাক্রমে Q ও R
$\therefore \mathrm{QR} \| \mathrm{BD}$ এবং $\mathrm{QR}=\frac{1}{2} \mathrm{BD}\ldots(ii)$
(i) ও (ii) থেকে পাই, $PS \| QR$ এবং $PS=QR$
$\therefore$ PQRS একটি সামান্তরিক। [$\because$ কোনো চতুর্ভুজের একজোড়া বিপরীত বাহু সমান ও সমান্তরাল হলে সেটি সামান্তরিক হয়।]
এখন, $\because$ ABCD একটি রম্বস,
$\therefore$ AB = AD
বা, $\frac{1}{2} \mathrm{AB}=\frac{1}{2} \mathrm{AD}$
বা, $\mathrm{AP}=\mathrm{AS}$
$\therefore \angle \mathrm{ASP}=\angle \mathrm{APS}=\theta$ (ধরি)
$\triangle \mathrm{APS}$-র $\angle \mathrm{PAS}=180^{\circ}-2 \theta$
ঠিক একইভাবে $\triangle \mathrm{SDR}$-র
$\angle D S R=\angle D R S=\phi$ (ধরি)
$\therefore \angle \mathrm{SDR}=180^{\circ}-2 \phi$
$\because$ ABCD রম্বস,
$\therefore 180^{\circ}-2 \theta+180^{\circ}-2 \phi=180^{\circ}$ [রম্বসের সমান্তরাল সরলরেখার একই পার্শ্বস্থ কোণদ্বয়ের সমষ্টি $180^{\circ}$]
বা, $2 \theta+2 \phi=180^{\circ}$
$\therefore \theta+\phi=90^{\circ}$
অর্থাৎ, $\angle \mathrm{PSA}+\angle \mathrm{DSR}=90^{\circ}$
$\therefore \angle \mathrm{PSR}=180^{\circ}-(\angle \mathrm{PSA}+\angle \mathrm{DSR})=180^{\circ}-90^{\circ}=90^{\circ}$
$\because$ PQRS সামান্তরিকের একটি কোণ $\angle \mathrm{PSR}=90^{\circ}$
$\therefore$ PQRS একটি আয়তাকার চিত্র। (প্রমাণিত)

প্রদত্ত : $\triangle \mathrm{ABC}$-র AB ও AC বাহুর মধ্যবিন্দু যথাক্রমে D ও E; P ও Q যথাক্রমে CD ও BD-র মধ্যবিন্দু।
প্রামাণ্য বিষয় : BE ও PQ পরস্পরকে সমদ্বিখণ্ডিত করে।
অঙ্কন : Q, E; E, P ও B, P যুক্ত করা হল।
প্রমাণ : $\because \triangle \mathrm{ADC}$-র CD ও AC-র মধ্যবিন্দু যথাক্রমে P ও E.
$\therefore P E \| A D$ এবং $P E=\frac{1}{2} A D$
বা, $P E \| A B$
বা, $P E=\frac{1}{2} B D\quad$ [$\because$ D, AB-র মধ্যবিন্দু]
$\therefore$ $P E \| B Q$
বা, $P E=B Q\quad$ [$\because$ Q, BD-র মধ্যবিন্দু]
[$\because$ AD, AB ও BQ একই সরলরেখাংশ]
এখন $\because$ BQEP চতুর্ভুজের $PE \| BQ$ এবং PE = BQ
$\therefore$ BQEP একটি সামান্তরিক যার BE ও QP দুটি কর্ণ।
$\because$ সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে।
$\therefore$ BE ও PQ পরস্পরকে সমদ্বিখণ্ডিত করবে। (প্রমাণিত)

প্রদত্ত : $\triangle \mathrm{ABC}$-র $\angle \mathrm{ABC}$-র সমদ্বিখণ্ডকের উপর AD লম্ব। D বিন্দু দিয়ে BC-র সমান্তরাল সরলরেখাংশ টানা হল, যা AC কে E বিন্দুতে ছেদ করে।
প্রামাণ্য বিষয় AE = EC অর্থাৎ E, AC-র মধ্যবিন্দু।
অঙ্কন : AD কে বর্ধিত করা হল, যা BC কে F বিন্দুতে ছেদ করে।
প্রমাণ : $\triangle \mathrm{ABD}$ ও $\triangle \mathrm{BDF}$-র
(i) $\angle A B D=\angle D B F$ [$\because B D, \angle A B C$-র সমদ্বিখণ্ডক]
(ii) BD সাধারণ বাহু
(iii) $\angle \mathrm{ADB}=\angle \mathrm{BDF}=\left(90^{\circ}\right)$
$\therefore$$\triangle \mathrm{ABD} \cong \triangle \mathrm{BDF}$
[A-S-A শর্তানুসারে]
$\therefore$ AD = DF, অর্থাৎ, D, AF-র মধ্যবিন্দু।
$\because$$DE \| BC$ (প্রদত্ত)
$\therefore$ E, AC-র মধ্যবিন্দু [$\because$ কোনো ত্রিভুজের একটি বাহুর মধ্যবিন্দু দিয়ে দ্বিতীয় বাহুর সমান্তরাল সরলরেখা টানলে তা তৃতীয় বাহুকে সমদ্বিখণ্ডিত করে।]
অর্থাৎ, AE = EC (প্রমাণিত)

প্রদত্ত : $\triangle A B C$-র AD মধ্যমা। B ও C বিন্দু দিয়ে AD-র সমান্তরাল সরলরেখাংশ যথাক্রমে BR ও CT টানা হল যারা বর্ধিত BA ও CA বাহুর সঙ্গে যথাক্রমে T ও R বিন্দুতে মিলিত হয়।
প্রামাণ্য বিষয় : $\frac{1}{\mathrm{AD}}=\frac{1}{\mathrm{RB}}+\frac{1}{\mathrm{TC}}$
প্রমাণ : $\because \triangle B R C$-র, BC-র মধ্যবিন্দু D এবং $AD \| BR$ হওয়ায়
$A D=\frac{1}{2} B R \ldots(i)$ [$\because$ কোনো ত্রিভুজের একটি বাহুর মধ্যবিন্দু দিয়ে দ্বিতীয় বাহুর সমান্তরাল সরলরেখা টানলে তা তৃতীয় বাহুকে সমদ্বিখণ্ডিত করে]
আবার, $\triangle \mathrm{BTC}$-র, BC-র মধ্যবিন্দু D এবং $AD \| CT$ হওয়ায়
$A D=\frac{1}{2} C T\ldots(ii)$ [$\because$ কোনো ত্রিভুজের একটি বাহুর মধ্যবিন্দু দিয়ে দ্বিতীয় বাহুর সমান্তরাল সরলরেখা টানলে তা তৃতীয় বাহুকে সমদ্বিখণ্ডিত করে]
(i) ও (ii) থেকে পাই, $\frac{1}{2} \mathrm{BR}=\frac{1}{2} \mathrm{CT}$
$\therefore \mathrm{BR}=\mathrm{CT}$
(i) থেকে পাই, $\frac{1}{\mathrm{AD}}=\frac{1}{\frac{1}{2} \mathrm{BR}}$
বা, $\frac{1}{\mathrm{AD}}=\frac{2}{\mathrm{BA}} \quad$
বা, $\frac{1}{\mathrm{AD}}=\frac{1}{\mathrm{BR}}+\frac{1}{\mathrm{BR}}$
$\therefore \frac{1}{\mathrm{AD}}=\frac{1}{\mathrm{BR}}+\frac{1}{\mathrm{TC}}\quad[\because \mathrm{BR}=\mathrm{TC}]$ (প্রমাণিত)

প্রদত্ত : ABCD ট্রাপিজিয়ামের $AB \| DC$ এবং AB > DC; E এবং F যথাক্রমে AC ও BD কর্ণদ্বয়ের মধ্যবিন্দু।
প্রামাণ্য বিষয় : $E F=\frac{1}{2}(A B-D C)$
অঙ্কন : C, F যুক্ত করে বর্ধিত করা হল, যা AB-কে G বিন্দুতে ছেদ করল।
প্ৰমাণ : $\because A B \| D C$ এবং BD ভেদক
$\therefore \angle C D B=\angle A B D\quad$[এরা একান্তর কোণ]
অর্থাৎ $\angle \mathrm{CDF}=\angle \mathrm{FBG}$
এখন $\triangle \mathrm{CDF}$ ও $\triangle \mathrm{FBG}$-র
(i) $\angle \mathrm{CDF}=\angle \mathrm{FBG}$
(ii) $\mathrm{DF}=\mathrm{FB}\quad$[$\because F, BD$-র মধ্যবিন্দু]
(iii) $\angle D F C=\angle B F G\quad$[এরা বিপ্রতীপ কোণ]
$\therefore \triangle \mathrm{CDF} \cong \triangle \mathrm{FBG}\quad$ [A-S-A শর্তানুসারে]
$\therefore$ CF = FG অর্থাৎ, F, CG-র মধ্যবিন্দু
এবং CD = GB
এখন $\triangle C A G$-র,
CG-র মধ্যবিন্দু F এবং AC-র মধ্যবিন্দু E
$\therefore E F=\frac{1}{2} A G$ [$\because$ ত্রিভুজের যে-কোনো দুই বাহুর মধ্যবিন্দুর সংযোজক রেখাংশ তৃতীয় বাহুর অর্ধেক]
$=\frac{1}{2}(A B-G B)$
$=\frac{1}{2}(A B-C D) \quad[\because \mathrm{GB}=\mathrm{CD}]$
$=\frac{1}{2}(A B-D C)$ (প্রমাণিত)

প্রদত্ত : AB সরলরেখাংশের মধ্যবিন্দু C এবং PQ যে-কোনো একটি সরলরেখা।
A, B ও C বিন্দু থেকে PQ সরলরেখার ক্ষুদ্রতম দূরত্ব যথাক্রমে AR, BS ও CT।
প্রামাণ্য বিষয় : AR + BS = 2CT
অঙ্কন : A, S যুক্ত করা হল যা CT কে O বিন্দুতে ছেদ করে।
প্রমাণ : A, B ও C থেকে PQ-এর ক্ষুদ্রতম দূরত্ব যথাক্রমে AR, BS ও CT।
$\therefore \mathrm{AR} \perp \mathrm{PQ}, \mathrm{BS} \perp \mathrm{PQ}$ এবং $\mathrm{CT} \perp \mathrm{PQ}$
অর্থাৎ, $\angle \mathrm{ARQ}=\angle \mathrm{BSQ}=\angle \mathrm{CTQ}=90^{\circ}$
$\because$ AR, BS ও CT একই সরলরেখা PQ-এর উপর লম্ব।
$\therefore AR \| BS \| CT$
এখন $\triangle \mathrm{ABS}$-এর AB-এর মধ্যবিন্দু C এবং $CO \| BS\quad [\because CT \| BS]$
$\therefore O, AS$-র মধ্যবিন্দু এবং $\mathrm{CO}=\frac{1}{2} \mathrm{BS}\ldots(i)$
আবার, $\triangle \mathrm{ASR}$-এর AS-এর মধ্যবিন্দু O এবং $OT \| AR\quad[\because CT \| AR]$
$\therefore O T=\frac{1}{2} A R\ldots(ii)$
(i) ও (ii) যোগ করে পাই, $\mathrm{CO}+\mathrm{OT}=\frac{1}{2} \mathrm{BS}+\frac{1}{2} \mathrm{AR}$
$\therefore C T=\frac{1}{2}(B S+A R)$
বা, $A R+B S=2 C T$ (প্রমাণিত)

প্রদত্ত : $\triangle \mathrm{ABC}$-র BC-র মধ্যবিন্দু D; PQ, A বিন্দুগামী সরলরেখা।
B, C ও D বিন্দু থেকে PQ-র উপর যথাক্রমে BL, CM ও DN লম্ব।
D, L ও D, M যুক্ত করা হল।
প্রামাণ্য বিষয় : DL = DM
প্রমাণ : $\because$ একই সরলরেখার PQ-র উপর BL, CM ও DN লম্ব
$\therefore BL \| CM \| DN$ এবং যেহেতু BC ও LM দুটি ভেদক, যেখানে BC-র মধ্যবিন্দু D
$\therefore$ LM এর মধ্যবিন্দু N হবে অর্থাৎ, LN = NM [কারণ যদি তিন বা ততোধিক সরলরেখাংশ একটি ভেদক থেকে সমান সমান অংশ খণ্ডিত করে তবে, তারা অপর একটি ভেদক থেকেও সমান সমান অংশ খণ্ডিত করে।]
এখন, $\triangle \mathrm{DNL}$ ও $\triangle \mathrm{DNM}$-র
(i) $\mathrm{LN}=\mathrm{NM}\quad$ [N, LM এর মধ্যবিন্দু]
(ii) $\angle D N L=\angle D N M\left(=90^{\circ}\right)$
(iii) DN সাধারণ বাহু
$\therefore \triangle \mathrm{DNL} \cong \triangle \mathrm{DNM}\quad$ [S-A-S শর্তানুসারে]
$\therefore$ DL = DM (প্রমাণিত)

প্রদত্ত : ABCD একটি বর্গাকার চিত্র।
AC ও BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করেছে।
$\angle B A C$-র সমদ্বিখণ্ডক BO কে P এবং BC কে Q বিন্দুতে ছেদ করেছে।
প্রামাণ্য বিষয় : $\mathrm{OP}=\frac{1}{2} \mathrm{CQ}$
অঙ্কন : C বিন্দু দিয়ে DB-র সমান্তরাল সরলরেখাংশ অঙ্কন করা হল, যা বর্ধিত AQ কে R বিন্দুতে ছেদ করে।
প্রমাণ : $\triangle \mathrm{ARC}$-র, AC-র মধ্যবিন্দু O $\quad[\because$ বর্গক্ষেত্রের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে$]$
এবং $OP \| CR\quad$ [$\because$ OP ও DB একই সরলরেখার অংশ]
$\therefore O P=\frac{1}{2} \mathrm{CR}\ldots(i)$ [$\because$ ত্রিভুজের যে-কোনো একটি বাহুর মধ্যবিন্দু দিয়ে দ্বিতীয় বাহুর সমান্তরাল সরলরেখা অঙ্কন করলে সমান্তরাল সরলরেখার খণ্ডিতাংশ তৃতীয় বাহুর অর্ধেক হবে।]
এখন $\because \angle \mathrm{BAC}$-র সমদ্বিখণ্ডক AQ
$\therefore \angle B A Q=\angle C A Q=\theta$ (ধরি)
$\therefore \triangle \mathrm{ARC}$-এর $\angle \mathrm{ARC}$
$=180^{\circ}-\angle \mathrm{CAR}-\angle \mathrm{ACR}$
$=180^{\circ}-\angle CAR -90^{\circ}$
$[\because$ $OP\|CR$ এবং AC ভেদক $\therefore \angle \mathrm{ACR}=\angle \mathrm{AOP}=90^{\circ}$ বর্গক্ষেত্রের কর্ণদ্বয় পরস্পর সমকোণে ছেদ করে।$]$
$=90^{\circ}-\theta\ldots(ii)$
আবার, $\triangle \mathrm{ABQ}$-র $\angle \mathrm{AQB}$
$=180^{\circ}-\angle \mathrm{BAQ}-\angle \mathrm{ABQ}$
$=180^{\circ}-\theta-90^{\circ}$
$=90^{\circ}-\theta\ldots(iii)$
$\therefore$ (ii) ও (iii) থেকে পাই,
$\angle A R C=\angle A Q B$
$\therefore \angle Q R C=\angle C Q R\quad [\because \angle A Q B=$ বিপ্রতীপ $\angle C Q R]$
$\therefore CQ=CR$
(i) থেকে পাই, $O P=\frac{1}{2} C R$
$\therefore \mathrm{OP}=\frac{1}{2} \mathrm{CQ}\quad[\because \mathrm{CR}=\mathrm{CQ}]$ (প্রমাণিত)

$\triangle P Q R$-এর $\triangle P Q R=90^{\circ}$ এবং অতিভুজ PR = 10 সেমি. এবং PR-এর মধ্যবিন্দু S।
$\therefore Q S=\frac{1}{2} P R$
$=\left(\frac{1}{2} \times 10 \right)$ সেমি.
= 5 সেমি.

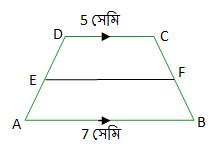
ABCD ট্রাপিজিয়ামের $AB \| DC$ এবং AD ও BC-র মধ্যবিন্দু যথাক্রমে E ও F।
$\therefore E F=\frac{1}{2}(A B+D C)$
$=\frac{1}{2}(7+5)$ সেমি
$=\left(\frac{1}{2} \times 12 \right)$ সেমি
= 6 সেমি

$\triangle \mathrm{ABC}$-র AD মধ্যমার মধ্যবিন্দু E; বর্ধিত BE, AC কে F বিন্দুতে ছেদ করে।
D বিন্দু দিয়ে $BF \| DG$ অঙ্কন করা হল, যা AC কে G বিন্দুতে ছেদ করে।
এখন $\triangle \mathrm{BFC}$-র BC-র মধ্যবিন্দু D এবং $BF \| DG,$
$\therefore CF$-র মধ্যবিন্দু G অর্থাৎ, FG = GC
আবার, $\triangle \mathrm{ADG}$-এর AD-এর মধ্যবিন্দু E এবং $EF \| GD$
$\therefore$ F, AG-র মধ্যবিন্দু অর্থাৎ, FG = AF
$\therefore A F=F G=G C$
$=\frac{1}{3}(A F+F G+G C)$
$=\frac{1}{3} \times A C$
$=\left(\frac{1}{3} \times 10.5\right)$ সেমি
= 3.5 সেমি

$\triangle \mathrm{ABC}$-র AB ও AC-র মধ্যবিন্দু যথাক্রমে F ও E
$\therefore FE \| BC$ এবং $F E=\frac{1}{2} B C=B D\ldots(i)$
$\therefore \mathrm{FE} \| \mathrm{BD}$
BDEF চতুর্ভুজটি একটি সামান্তরিক যার কর্ণদ্বয় BE ও FD পরস্পরকে $X$ বিন্দুতে সমদ্বিখণ্ডিত করে।
$\therefore$ ED-র মধ্যবিন্দু Y $\quad[\because \Delta E F D$ -এর $X, FD$-র মধ্যবিন্দু এবং $XY \| EF]$
এখন, $\triangle E F D$-র FD-র মধ্যবিন্দু $X$ এবং ED-র মধ্যবিন্দু Y
$\therefore X Y=\frac{1}{2} \mathrm{FE}$
$=\frac{1}{2} \cdot \frac{1}{2} \mathrm{BC}\quad$ [(i) থেকে পাই]
$=\frac{1}{4} \mathrm{BC}$

$\triangle D C E$ ও $\triangle \mathrm{BEF}$-র
(i) $C E=B E\quad$ [$\because$ E, BC-র মধ্যবিন্দু]
(ii) $\angle \mathrm{DEC}=\angle \mathrm{BEF}\quad$[বিপ্রতীপ কোণ]
(iii) $\angle D C E=$ একান্তর $\angle E B F\quad$ [$\because DC \| BF , BC$ ভেদক]
$\triangle D C E \cong \triangle B E F\quad$ [A-S-A শর্তানুসারে]
$DC = BF\quad$ (সর্বসম ত্রিভুজের অনুরূপ বাহু)
$\therefore A F=A B+B F$
$=A B+D C\quad[\because D C=B F]$
$=A B+A B\quad[\because A B=D C]$
$=2 A B$

প্রদত্ত শর্তানুযায়ী, BC-এর মধ্যবিন্দু D এবং AC-এর মধ্যবিন্দু E।
$C E=\frac{1}{2} A C=\left(\frac{1}{2} \times 8\right)$ সেমি = 4 সেমি
এখন, $\triangle B C E$-এর, BC বাহুর মধ্যবিন্দু D এবং
$DF \| BE$ (প্রদত্ত)
$\therefore$ CE বাহুর মধ্যবিন্দু F
$\therefore C F=\frac{1}{2} C E=\left(\frac{1}{2} \times 4\right)$ সেমি = 2 সেমি।

$\because$ AB-এর মধ্যবিন্দু R
$A R=\frac{1}{2} A B=\left(\frac{1}{2} \times 30 \right)$ সেমি = 15 সেমি
আবার, AC বাহুর মধ্যবিন্দু Q
$A Q=\frac{1}{2} A C=\left(\frac{1}{2} \times 21\right)$ সেমি
= 10.5 সেমি
এখন, $\triangle \mathrm{ABC}$-এর BC ও AC বাহুর মধ্যবিন্দু যথাক্রমে P ও Q।
$\therefore P Q=\frac{1}{2} A B=\left(\frac{1}{2} \times 30 \right)$ সেমি = 15 সেমি
আবার, $\triangle \mathrm{ABC}$-এর AB ও BC বাহুর মধ্যবিন্দু যথাক্রমে R ও P
$\therefore R P=\frac{1}{2} A C=\left(\frac{1}{2} \times 21\right)$ সেমি
= 10.5 সেমি
$\therefore$ ARPQ চতুর্ভুজের পরিসীমা = (AR + RP + PQ + QA)
= (15 + 10.5 + 15 + 10.5) সেমি
= 51 সেমি

B ও D যোগ করা হল।
এখন, $\triangle A B D$-এর AB ও AD বাহুদ্বয়ের মধ্যবিন্দু যথাক্রমে $P$ ও $X$ ।
$\therefore P X=\frac{1}{2} B D\ldots(i)$
আবার, $\triangle \mathrm{BCD}$-এর BC ও DC বাহুদ্বয়ের মধ্যবিন্দু যথাক্রমে Q ও Y
$\therefore Q Y=\frac{1}{2} B D$
সুতরাং, (i) ও (ii) থেকে পাই, $PX = QY$
$\therefore$ QY = 5 সেমি $\quad[\because PX = 5$ সেমি$]$

$\triangle \mathrm{BGC}$-এর BG ও GC বাহুদ্বয়ের মধ্যবিন্দু যথাক্রমে P ও Q।
$\therefore P Q=\frac{1}{2} B C$
বা, BC = 2PQ
$\therefore B C=(2 \times 3)$ সেমি = 6 সেমি।

$\triangle \mathrm{ABC}$-এর মধ্যে AB ও AC-এর মধ্যবিন্দু যথাক্রমে F ও E।
$\therefore$ $FE \| BC$ এবং $\mathrm{FE}=\frac{1}{2} \mathrm{BC}$
আবার, $\triangle \mathrm{ABD}$-এর AB বাহুর মধ্যবিন্দু F
এবং $FO \| BD\quad [\because FE \| BC]$
$\therefore$ O, AD এর মধ্যবিন্দু।
$\therefore \mathrm{AO}=\frac{1}{2} \mathrm{AD}=\left(\frac{1}{2} \times 6\right)$ সেমি = 3 সেমি